题目内容
 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=| 3 |
(1)若在边BC上存在点Q,且使得PQ⊥QD,求a的取值范围;
(2)当BC边上存在唯一点Q,使PQ⊥QD时,求异面直线AQ与PD所成角的大小.
分析:(1)分别以AD、AB、AP所在直线为x、y、z轴,建立空间直角坐标系.可得B、C、D、P各点的坐标,设Q的坐标为(t,
,0),可得
、
关于a、t的坐标,由
•
=0,建立关于a、t的关系式得t2-at+3=0,由根的判别式即可解出实数a的范围;
(2)根据点Q唯一,结合(1)的结论得a=2
且t=
,由此可得
、
的坐标,利用空间向量的夹角公式算出cos<
,
>=
,即可得到异面直线AQ与PD所成角的大小.
| 3 |
| PQ |
| DQ |
| PQ |
| DQ |
(2)根据点Q唯一,结合(1)的结论得a=2
| 3 |
| 3 |
| AQ |
| PD |
| AQ |
| PD |
| ||
| 14 |
解答:解:(1)分别以AD、AB、AP所在直线为x、y、z轴,建立空间直角坐标系,如图所示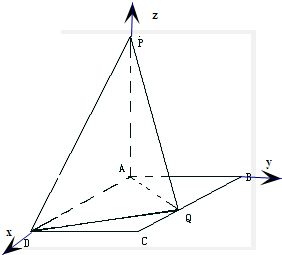
则B(0,
,0),C(a,
,0),D(a,0,0),
P(0,0,4)
设Q(t,
,0),可得
=(t,
,-4),
=(t-a,
,0)
∵PQ⊥DQ,∴
•
=t(t-a)+3=0,即t2-at+3=0
因此,△=a2-12≥0,解之得a≥2
;
(2)∵边BC上存在唯一的点Q,使得PQ⊥QD,
∴由(1)得a=2
,t=
可得Q(
,
,0),
=(
,
,0),
=(2
,0,-4)
∴cos<
,
>=
=
=
因此,异面直线AQ与PD所成角的大小为arccos
.

则B(0,
| 3 |
| 3 |
P(0,0,4)
设Q(t,
| 3 |
| PQ |
| 3 |
| DQ |
| 3 |
∵PQ⊥DQ,∴
| PQ |
| DQ |
因此,△=a2-12≥0,解之得a≥2
| 3 |
(2)∵边BC上存在唯一的点Q,使得PQ⊥QD,
∴由(1)得a=2
| 3 |
| 3 |
可得Q(
| 3 |
| 3 |
| AQ |
| 3 |
| 3 |
| PD |
| 3 |
∴cos<
| AQ |
| PD |
| ||||
|
| 6 | ||||
|
| ||
| 14 |
因此,异面直线AQ与PD所成角的大小为arccos
| ||
| 14 |
点评:本题给出底面为矩形的线面垂直的几何体,探索满足条件的线线垂直并依此求异面直线所成角.着重考查了利用空间向量研究线线垂直和求异面直线所成角的大小等知识,属于中档题.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD.
如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD. 如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.
如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点. 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=