网址：http://m.1010jiajiao.com/timu_id_425169[举报]
| 1 |
| x |
| 2 |
| y |
| xy |
| 1 | ||
|
| 1 |
| x |
| 2 |
| y |
|
| 1 |
| x |
| 2 |
| y |
| 2 |
| 2 |
若某产品的直径长与标准值的差的绝对值不超过1mm 时，则视为合格品，否则视为不合格品。在近期一次产品抽样检查中，从某厂生产的此种产品中，随机抽取5000件进行检测，结果发现有50件不合格品。计算这50件不合格品的直径长与标准值的差（单位：mm）, 将所得数据分组，得到如下频率分布表：
|
分组 |
频数 |
频率 |
|
[-3, -2) |
|
0.10 |
|
[-2, -1) |
8 |
|
|
（1,2] |
|
0.50 |
|
（2,3] |
10 |
|
|
（3,4] |
|
|
|
合计 |
50 |
1．00 |
（Ⅰ）将上面表格中缺少的数据填在答题卡的相应位置；
（Ⅱ）估计该厂生产的此种产品中，不合格品的直径长与标准值的差落在区间（1,3]内的概率；
（Ⅲ）现对该厂这种产品的某个批次进行检查，结果发现有20件不合格品。据此估算这批产品中的合格品的件数。
【解析】（Ⅰ）
|
分组 |
频数 |
频率 |
|
[-3, -2) |
5 |
0.10 |
|
[-2, -1) |
8 |
0.16 |
|
（1,2] |
25 |
0.50 |
|
（2,3] |
10 |
0.2 |
|
（3,4] |
2 |
0.04 |
|
合计 |
50 |
1．00 |
（Ⅱ）根据频率分布表可知，落在区间（1,3]内频数为35，故所求概率为0.7.
（Ⅲ）由题可知不合格的概率为
0.01，故可求得这批产品总共有2000，故合格的产品有1980件。
查看习题详情和答案>>
| 1 |
| x |
| 2 |
| y |
| xy |
| 1 | ||
|
| 1 |
| x |
| 2 |
| y |
|
| 1 |
| x |
| 2 |
| y |
| 2 |
| 2 |
求圆心在直线y＝－2x上，并且经过点A(2,－1)，与直线x＋y＝1相切的圆的方程.
【解析】利用圆心和半径表示圆的方程，首先
设圆心为S，则KSA＝1,∴SA的方程为：y＋1＝x－2，即y＝x－3， ………4分
和y＝－2x联立解得x＝1,y＝－2，即圆心(1,－2)
∴r＝
＝
,
故所求圆的方程为：
＋
＝2
解：法一：
设圆心为S，则KSA＝1,∴SA的方程为：y＋1＝x－2，即y＝x－3， ………4分
和y＝－2x联立解得x＝1,y＝－2，即圆心(1,－2) ……………………8分
∴r＝＝,
………………………10分
故所求圆的方程为：＋＝2
………………………12分
法二：由条件设所求圆的方程为：
＋
＝
, ………………………6分
解得a＝1,b＝－2, ＝2
………………………10分
所求圆的方程为：＋＝2
………………………12分
其它方法相应给分
查看习题详情和答案>>
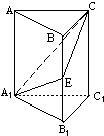
（1）求证：BE=EB1；
（2）若AA1=A1B1；求平面A1EC与平面A1B1C1所成二面角（锐角）的度数．
注意：在下面横线上填写适当内容，使之成为（Ⅰ）的完整证明，并解答（Ⅱ）．
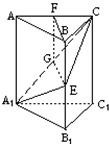
（1）证明：在截面A1EC内，过E作EG⊥A1C，G是垂足．
①∵
∴EG⊥侧面AC1；取AC的中点F，连接BF，FG，由AB=BC得BF⊥AC，
②∵
∴BF⊥侧面AC1；得BF∥EG，BF、EG确定一个平面，交侧面AC1于FG．
③∵
∴BE∥FG，四边形BEGF是平行四边形，BE=FG，
④∵
∴FG∥AA1，△AA1C∽△FGC，
⑤∵
∴FG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |