摘要：(Ⅲ)取MN的中点G.连结AG.BG.如图9―71∵AM=AN.BM=BN.G为MN的中点∴AG⊥MN.BG⊥MN.∠AGB即为二面角α的平面角.
网址：http://m.1010jiajiao.com/timu_id_425166[举报]
（（本小题满分13分）
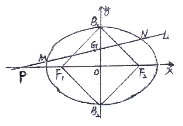
已知椭圆C的中心在原点，焦点在X轴上，以两个焦点和短轴的两个端点为顶点的四边形
是一个面积为8的正方形.
求椭圆C的方程；
设P是椭圆C的左准线与X轴的交点，过点P的直线L与椭圆C相交于M，N两点.当线段MN的中点G落在正方形内（包括边界）时，求直线L的斜率的取值范围.
查看习题详情和答案>>
已知椭圆C的中心在原点,焦点在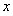
轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
(1)求椭圆C的方程;
(2)已知点P的坐标为P(－4,0), 过P点的直线L与椭圆C相交于M、N两点,当线段MN的中点G落在正方形内(包含边界)时,求直线L的斜率的取值范围.
查看习题详情和答案>>
已知圆心为C的圆经过点A（-3，0）和点B（1，0）两点，且圆心C在直线y=x+1上．
（1）求圆C的标准方程．
（2）已知线段MN的端点M的坐标（3，4），另一端点N在圆C上运动，求线段MN的中点G的轨迹方程；
（3）是否存在斜率为1的直线l，使l被圆C截得的弦PQ，且以PQ为直径的圆经过坐标原点？若存在求出直线l的方程，若不存在说明理由． 查看习题详情和答案>>
（1）求圆C的标准方程．
（2）已知线段MN的端点M的坐标（3，4），另一端点N在圆C上运动，求线段MN的中点G的轨迹方程；
（3）是否存在斜率为1的直线l，使l被圆C截得的弦PQ，且以PQ为直径的圆经过坐标原点？若存在求出直线l的方程，若不存在说明理由． 查看习题详情和答案>>