题目内容
已知椭圆C的中心在原点,焦点在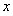 轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
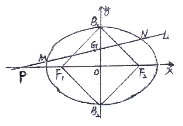
(1)求椭圆C的方程;
(2)已知点P的坐标为P(-4,0), 过P点的直线L与椭圆C相交于M、N两点,当线段MN的中点G落在正方形内(包含边界)时,求直线L的斜率的取值范围.
【答案】
(1)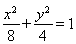 ;(2)
;(2)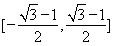
【解析】
试题分析:(1)依题意需要求椭圆的标准方程,所以要找到两个关于基本量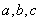 的等式,由
的等式,由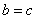 以及面积的关系可求椭圆的方程.
以及面积的关系可求椭圆的方程.
(2)由于直线与椭圆的相交得到的弦的中点坐标,可通过假设直线方程与椭圆的方程联立可求得,判别式要大于零.其中用直线的斜率表示中点坐标.由于中点在正方形内,其实就是要符合一个不等式的可行域问题.因此通过解不等式即可得到所求的结论.
试题解析:(1)求得椭圆C的方程为;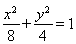 ;
;
(2)∵点P的坐标为(-4,0),显然直线L的斜率k存在,
∴直线L方程为 如图设点M、N的坐标分别为
如图设点M、N的坐标分别为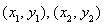 ,
,
线段MN的中点为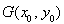 ,由
,由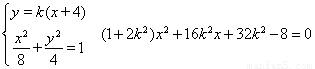
由△>0解得: 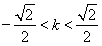 又
又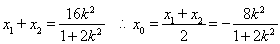
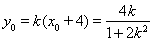 , ∵
, ∵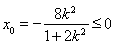 , ∴点G不可能在y轴的右边,
, ∴点G不可能在y轴的右边,
又直线F1B2, F1B1的方程分别为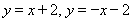 .
.
∴点G在正方形B1F2B1F1内的充要条件为:  即
即
即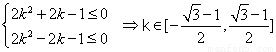 .
.
考点:1.椭圆的性质.2.直线与椭圆的位置关系.3.线性规划的知识.4.韦达定理.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

 。
。