摘要:∴∠B1PG=arctan.即所求二面角的大小为arctan.(Ⅱ)证明:∵AB.CD是矩形ABCD的一组对边.有AB∥CD.又CD是面ABCD与面CDEF的交线.∴AB∥面CDEF. ∵EF是面ABFE与面CDEF的交线.∴AB∥EF. ∵AB是平面ABCD内的一条直线.EF在平面ABCD外.∴EF∥面ABCD.(Ⅲ)V估<V.证明:∵a>c.b>d.
网址:http://m.1010jiajiao.com/timu_id_425148[举报]
已知x,y∈R+且x+y=4,求
+
的最小值.某学生给出如下解法:由x+y=4得,4≥2
①,即
≥
②,又因为
+
≥2
③,由②③得
+
≥
④,即所求最小值为
⑤.请指出这位同学错误的原因 .
查看习题详情和答案>>
| 1 |
| x |
| 2 |
| y |
| xy |
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| x |
| 2 |
| y |
|
| 1 |
| x |
| 2 |
| y |
| 2 |
| 2 |
已知x>0,y>0且x+y=4,求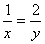 的最小值.某学生给出如下解法:由x+y=4,得4≥2
的最小值.某学生给出如下解法:由x+y=4,得4≥2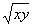 ①,即
①,即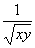 ≥
≥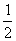 ②,又因为
②,又因为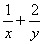 ≥2
≥2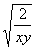 ③,由②③得
③,由②③得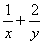 ≥
≥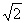 ④,即所求最小值为
④,即所求最小值为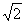 ⑤.请指出这位同学错误的原因:__________.
查看习题详情和答案>>
⑤.请指出这位同学错误的原因:__________.
查看习题详情和答案>>
已知x,y∈R+且x+y=4,求
+
的最小值.某学生给出如下解法:由x+y=4得,4≥2
①,即
≥
②,又因为
+
≥2
③,由②③得
+
≥
④,即所求最小值为
⑤.请指出这位同学错误的原因______.
查看习题详情和答案>>
| 1 |
| x |
| 2 |
| y |
| xy |
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| x |
| 2 |
| y |
|
| 1 |
| x |
| 2 |
| y |
| 2 |
| 2 |
已知函数 。
。
(1)求函数的最小正周期和最大值;
(2)求函数的增区间;
(3)函数的图象可以由函数 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
【解析】本试题考查了三角函数的图像与性质的运用。第一问中,利用 可知函数的周期为
可知函数的周期为 ,最大值为
,最大值为 。
。
第二问中,函数 的单调区间与函数
的单调区间与函数 的单调区间相同。故当
的单调区间相同。故当 ,解得x的范围即为所求的区间。
,解得x的范围即为所求的区间。
第三问中,利用图像将 的图象先向右平移
的图象先向右平移 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的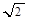 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。
解:(1)函数 的最小正周期为
的最小正周期为 ,最大值为
,最大值为 。
。
(2)函数 的单调区间与函数
的单调区间与函数 的单调区间相同。
的单调区间相同。
 即
即
 所求的增区间为
所求的增区间为 ,
,
 即
即
 所求的减区间为
所求的减区间为 ,
, 。
。
(3)将 的图象先向右平移
的图象先向右平移 个单位长度,再把横坐标缩短为原来的
个单位长度,再把横坐标缩短为原来的 (纵坐标不变),然后把纵坐标伸长为原来的
(纵坐标不变),然后把纵坐标伸长为原来的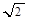 倍(横坐标不变),再向上平移1个单位即可。
倍(横坐标不变),再向上平移1个单位即可。
查看习题详情和答案>>
 与直线
与直线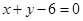 及
及 所围成图形的面积.
所围成图形的面积. ,所以得到
,所以得到 ,由此得到结论为
,由此得到结论为
 ,则
,则