摘要：(Ⅰ)证明:∵∠SAB=∠SAC=90°. ∴SA⊥AB.SA⊥AC.又AB∩AC=A. ∴SA⊥平面ABC.由于∠ACB=90°.即BC⊥AC. 由三垂线定理.得SC⊥BC.(Ⅱ)解:∵BC⊥AC.SC⊥BC∴∠SCA是侧面SCB与底面ABC所成二面角的平面角.
网址：http://m.1010jiajiao.com/timu_id_425115[举报]
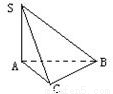
在三棱锥S-ABC中，∠SAB=∠SAC=∠ACB=90°，且AC=BC=5，SB=5| 5 |
（Ⅰ）证明：SC⊥BC；
（Ⅱ）求侧面SBC与底面ABC所成二面角的大小；
（Ⅲ）求三棱锥的体积VS-ABC．
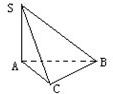在三棱锥S-ABC中，如图，∠SAB=∠SAC=∠ACB=90°，AC=2，BC=
| 13 |
| 29 |
（1）证明：SC⊥BC；
（2）求侧面SBC与底面ABC所成的二面角大小；
（3）（理）求异面直线SC与AB所成的角的大小（用反三角函数表示）．
（文）求三棱锥的体积VS-ABC． 查看习题详情和答案>>
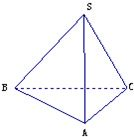在三棱锥S-ABC中，∠SAB=∠SAC=∠ACB=90°，AC=1，BC=| 3 |
| 3 |
（1）求三棱锥S-ABC的体积；
（2）证明：BC⊥SC；
（3）求异面直线SB和AC所成角的余弦值． 查看习题详情和答案>>
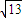，SB=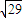
．
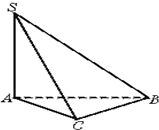在三棱锥S-ABC中，∠SAB=∠SAC=∠ACB=90°，且AC=BC=5，SB=5
．