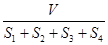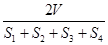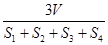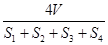摘要：∴4R2＝ R＝ 又∵球的体积为V＝πR 3
网址：http://m.1010jiajiao.com/timu_id_425050[举报]
已知圆的面积S（R）=πR2，显然S'（R）=2πR表示的是圆的周长，即C=2πR把该结论类比到空间，写出球中的类似结论：
查看习题详情和答案>>
以半径为R的球的体积为V(R)=
πR3，其导函数表示的是球的表面积，即S=4πR2．
| 4 |
| 3 |
以半径为R的球的体积为V(R)=
πR3，其导函数表示的是球的表面积，即S=4πR2．
．| 4 |
| 3 |
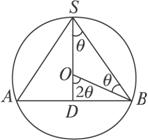
设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r ，则r＝
；类比这个结论可知：四面体S－ABC的四个面的面积分别为S1、S2、S3、S4，内切球的半径为R，四面体P－ABC的体积为V，则R＝( )
A．
B．
C．
D．
查看习题详情和答案>>
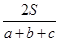；类比这个结论可知：四面体S－ABC的四个面的面积分别为S1、S2、S3、S4，内切球的半径为R，四面体P－ABC的体积为V，则R＝( )
