题目内容
已知圆的面积S(R)=πR2,显然S'(R)=2πR表示的是圆的周长,即C=2πR把该结论类比到空间,写出球中的类似结论:
以半径为R的球的体积为V(R)=
πR3,其导函数表示的是球的表面积,即S=4πR2.
| 4 |
| 3 |
以半径为R的球的体积为V(R)=
πR3,其导函数表示的是球的表面积,即S=4πR2.
.| 4 |
| 3 |
分析:圆的面积函数的导数等于圆的周长函数,类比得到球的体积函数的导数等于球的表面积函数,由二维空间推广到三维空间.
解答:解:由类比思想,可得半径为R的球的体积为V(R)=
πR3,其导函数为V′(R)=
×3πR2=4πR2,显然表示的是球的表面积.
故答案为:以半径为R的球的体积为V(R)=
πR3,其导函数表示的是球的表面积,即S=4πR2.
| 4 |
| 3 |
| 4 |
| 3 |
故答案为:以半径为R的球的体积为V(R)=
| 4 |
| 3 |
点评:本题考查类比推理,解答本题的关键是:(1)找出两类事物:圆与球之间的相似性或一致性;(2)用圆的性质去推测球的性质.

练习册系列答案
相关题目
 的方程为
的方程为 ,过点
,过点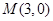 作直线与圆
作直线与圆 、
、 两点。
两点。
 ,求直线AB的方程;
,求直线AB的方程; 的面积最大时,求直线AB的斜率;
的面积最大时,求直线AB的斜率; 作两条直线与圆O分别交于R、S,若
作两条直线与圆O分别交于R、S,若 ,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。
,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。