摘要:故不存在常数C<0.使=lg(Sn+1-C).评述:本题为综合题.以数列为核心知识.在考查等比数列基本知识的同时.考查不等式的证明和解方程.兼考对数的运算法则和对数函数的单调性.并且多角度.多层次考查数学思想方法的灵活.恰当的运用.提高对数学能力的考查要求.该题的解答方法很多.表明该题能较好考查灵活综合运用数学知识的能力.第(Ⅰ)问侧重知识和基本技能的考查.第(Ⅱ)问则把考查的重心放在能力要求上.对思维的逻辑性.周密性和深刻性,运算的合理性.准确性,应用的灵活性.有效性等.该题都涉及到了.是一道突出能力考查的好试题.
网址:http://m.1010jiajiao.com/timu_id_422777[举报]
设{an}是由正数组成的等比数列,Sn是其前n项和.
(1)证明
<lgSn+1;
(2)是否存在常数c>0,使得
=lg(Sn+1-c)成立?并证明你的结论.
查看习题详情和答案>>
(1)证明
| lgSn+lgSn+2 |
| 2 |
(2)是否存在常数c>0,使得
| lg(Sn-c)+lg(Sn+2-c) |
| 2 |
设{an}是由正数组成的等比数列,Sn是其前n项和.
(1)证明
<lgSn+1;
(2)是否存在常数c>0,使得
=lg(Sn+1-c)成立?并证明你的结论.
查看习题详情和答案>>
(1)证明
| lgSn+lgSn+2 |
| 2 |
(2)是否存在常数c>0,使得
| lg(Sn-c)+lg(Sn+2-c) |
| 2 |
(2011•东城区二模)已知a,b为两个正数,且a>b,设a1=
,b1=
,当n≥2,n∈N*时,an=
,bn=
.
(Ⅰ)求证:数列{an}是递减数列,数列{bn}是递增数列;
(Ⅱ)求证:an+1-bn+1<
(an-bn);
(Ⅲ)是否存在常数C>0使得对任意n∈N*,有|an-bn|>C,若存在,求出C的取值范围;若不存在,试说明理由.
查看习题详情和答案>>
| a+b |
| 2 |
| ab |
| an-1+bn-1 |
| 2 |
| an-1bn-1 |
(Ⅰ)求证:数列{an}是递减数列,数列{bn}是递增数列;
(Ⅱ)求证:an+1-bn+1<
| 1 |
| 2 |
(Ⅲ)是否存在常数C>0使得对任意n∈N*,有|an-bn|>C,若存在,求出C的取值范围;若不存在,试说明理由.
已知a,b为两个正数,且a>b,设a1= ,b1=
,b1=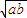 ,当n≥2,n∈N*时,an=
,当n≥2,n∈N*时,an= ,bn=
,bn= .
.
(Ⅰ)求证:数列{an}是递减数列,数列{bn}是递增数列;
(Ⅱ)求证:an+1-bn+1< (an-bn);
(an-bn);
(Ⅲ)是否存在常数C>0使得对任意n∈N*,有|an-bn|>C,若存在,求出C的取值范围;若不存在,试说明理由.
查看习题详情和答案>>
查看习题详情和答案>>
 ,b1=
,b1=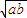 ,当n≥2,n∈N*时,an=
,当n≥2,n∈N*时,an= ,bn=
,bn= .
.(Ⅰ)求证:数列{an}是递减数列,数列{bn}是递增数列;
(Ⅱ)求证:an+1-bn+1<
 (an-bn);
(an-bn);(Ⅲ)是否存在常数C>0使得对任意n∈N*,有|an-bn|>C,若存在,求出C的取值范围;若不存在,试说明理由.
查看习题详情和答案>>
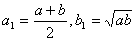 ,当n≥2,n∈N*时,
,当n≥2,n∈N*时,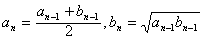 。
。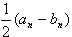 ;
;