摘要:答案:
网址:http://m.1010jiajiao.com/timu_id_422015[举报]
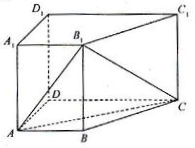 (2013•福建)如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)
(2013•福建)如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)(1)求证:CD⊥平面ADD1A1
(2)若直线AA1与平面AB1C所成角的正弦值为
| 6 | 7 |
(3)现将与四棱柱ABCD-A1B1C1D1形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为f(k),写出f(k)的解析式.(直接写出答案,不必说明理由)
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先将右面给出的程序框图补充完整,再将与其功能相当的程序语言补充完整,把答案写在下面空格上。
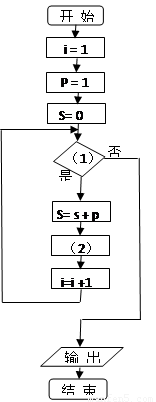
程序语言:
i=1
p=1
s=0
DO
s=" s" + p
(2)
i=i+1
(3)
PRINT s
END
(1)_________ (2)______ (3)
查看习题详情和答案>>
函数y=ax+1(a≠0,-1≤x≤1)的值域是
查看习题详情和答案>>
a>0时,答案为:[1-a,1+a]
a<0时,答案为:[1+a,1-a].
a<0时,答案为:[1+a,1-a].
a>0时,答案为:[1-a,1+a]
a<0时,答案为:[1+a,1-a].
.a<0时,答案为:[1+a,1-a].
(2007•上海模拟)(1)若直角三角形两直角边长之和为12,求其周长p的最小值;
(2)若三角形有一个内角为arccos
,周长为定值p,求面积S的最大值;
(3)为了研究边长a,b,c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:16S2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=[(a+b)2-c2][c2-(a-b)2]=-c4+2(a2+b2)c2-(a2-b2)2=-[c2-(a2+b2)]2+4a2b2
而-[c2-(a2+b2)]2≤0,a2≤81,b2≤64,则S≤36,但是,其中等号成立的条件是c2=a2+b2,a=9,b=8,于是c2=145与3≤c≤4矛盾,所以,此三角形的面积不存在最大值.
以上解答是否正确?若不正确,请你给出正确的答案.
(注:16S2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)称为三角形面积的海伦公式,它已经被证明是正确的)
查看习题详情和答案>>
(2)若三角形有一个内角为arccos
| 7 | 9 |
(3)为了研究边长a,b,c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值,现有解法如下:16S2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=[(a+b)2-c2][c2-(a-b)2]=-c4+2(a2+b2)c2-(a2-b2)2=-[c2-(a2+b2)]2+4a2b2
而-[c2-(a2+b2)]2≤0,a2≤81,b2≤64,则S≤36,但是,其中等号成立的条件是c2=a2+b2,a=9,b=8,于是c2=145与3≤c≤4矛盾,所以,此三角形的面积不存在最大值.
以上解答是否正确?若不正确,请你给出正确的答案.
(注:16S2=(a+b+c)(a+b-c)(a-b+c)(-a+b+c)称为三角形面积的海伦公式,它已经被证明是正确的)
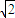 =0与圆C:x2+y2=2相切,且满足上述条件的直线l共有n条,则n的值为( )
=0与圆C:x2+y2=2相切,且满足上述条件的直线l共有n条,则n的值为( )