网址:http://m.1010jiajiao.com/timu_id_414620[举报]
1.B 解析:.files/image003.gif) 转变成可裂变的
转变成可裂变的.files/image005.gif) (金属钚),质量数增加1,一定是吸收一个快中子变成铀239,再转变成
(金属钚),质量数增加1,一定是吸收一个快中子变成铀239,再转变成.files/image005.gif) 时核电荷数增加2,因此是发生了两次β衰变,AC错B正确;钚239是中子数为239-94=145,铀238的中子数为238-92=146,因此钚239比铀238少一个中子,D错。
时核电荷数增加2,因此是发生了两次β衰变,AC错B正确;钚239是中子数为239-94=145,铀238的中子数为238-92=146,因此钚239比铀238少一个中子,D错。
2.B 解析:随水银柱上升,水银柱的长度变短,气体压强变小,当水银被全部推出管外后,气体压强等于大气压强为最小,A错;水银柱缓慢上升时,气体温度升高,内能增大,同时气体体积增大,对外做功,由.files/image182.gif) 可知,
可知,.files/image184.gif) ,B正确;在水银被从管中突然全部推出过程中,气体迅速膨胀对外做功,但吸热较慢因此气体的内能一定减小,C错;若在端面a上升到
,B正确;在水银被从管中突然全部推出过程中,气体迅速膨胀对外做功,但吸热较慢因此气体的内能一定减小,C错;若在端面a上升到.files/image008.gif) 前停止加热,气体温度下降,V减小,水银柱下降,但当气体温度回到初始状态时,压强比初始状态小,气体柱比初始状态长,D错。
前停止加热,气体温度下降,V减小,水银柱下降,但当气体温度回到初始状态时,压强比初始状态小,气体柱比初始状态长,D错。
.files/image186.gif) 3.AC 解析:由图可知,
3.AC 解析:由图可知,.files/image021.gif) 车的初速度等于
车的初速度等于.files/image189.gif) ,在
,在.files/image031.gif) 时间内,
时间内,.files/image021.gif) 车的位移为
车的位移为.files/image028.gif) ,则
,则.files/image019.gif) 车的位移为
车的位移为.files/image195.gif) 。若
。若.files/image013.gif) 在
在.files/image031.gif) 时刻相遇,则
时刻相遇,则.files/image199.gif) ,A项正确;若
,A项正确;若.files/image013.gif) 在
在.files/image036.gif) 时刻相遇,由图象可知,
时刻相遇,由图象可知,.files/image028.gif) 为阴影部分对应的距离,即
为阴影部分对应的距离,即.files/image204.gif) ,由图象中的对称关系,下次相遇的时刻为
,由图象中的对称关系,下次相遇的时刻为.files/image206.gif) ,C正确B项错;若
,C正确B项错;若.files/image013.gif) 在
在.files/image031.gif) 时刻相遇,之后
时刻相遇,之后.files/image210.gif) ,不能再次相遇,D错。
,不能再次相遇,D错。
.files/image211.gif) 4.B 解析:在物块下滑过程中重力对物块的冲量为15N?s,故下滑时间为
4.B 解析:在物块下滑过程中重力对物块的冲量为15N?s,故下滑时间为.files/image213.gif) s,斜面对物块的支持力
s,斜面对物块的支持力.files/image215.gif) N,故支持力的冲量
N,故支持力的冲量.files/image217.gif) ,A错;物块从静止下滑,斜面对物块的滑动摩擦力
,A错;物块从静止下滑,斜面对物块的滑动摩擦力.files/image219.gif) N,其冲量为
N,其冲量为.files/image221.gif) ,B正确;斜面对物块的作用力一定小于物块的重力,所以其冲量一定小于重力的冲量,C错;物块到达斜面底端时的动量等于外力的总冲量,一定小于重力的冲量,D错。
,B正确;斜面对物块的作用力一定小于物块的重力,所以其冲量一定小于重力的冲量,C错;物块到达斜面底端时的动量等于外力的总冲量,一定小于重力的冲量,D错。
5.C 解析:水流做平抛运动,水平位移.files/image223.gif) ,代入
,代入.files/image056.gif) 解得
解得.files/image226.gif) ,即得
,即得.files/image228.gif) (d>0,舍去),因此当H一定时,
(d>0,舍去),因此当H一定时,.files/image230.gif) 与
与.files/image054.gif) 有关,A错;若
有关,A错;若.files/image054.gif) 一定,则H减小时d增大,B错;若H一定,
一定,则H减小时d增大,B错;若H一定,.files/image054.gif) 增大时,d也应该增大,C正确;若d一定,H减小时,
增大时,d也应该增大,C正确;若d一定,H减小时,.files/image054.gif) 应该减小,D错。
应该减小,D错。
.files/image235.gif)
.files/image236.gif) 6.ACD 解析:对A、B整体和P,受力如图(a)(b),其中
6.ACD 解析:对A、B整体和P,受力如图(a)(b),其中.files/image238.gif)
.files/image240.gif) ,
, .files/image242.gif)
.files/image244.gif) 。若保持B的半径
。若保持B的半径.files/image072.gif) 不变,而将B改变密度较大的材料制作,则
不变,而将B改变密度较大的材料制作,则.files/image153.gif) 角不变而B的质量增大,
角不变而B的质量增大,.files/image248.gif) 均增大,A正确;对B,受力如图(c),
均增大,A正确;对B,受力如图(c),.files/image250.gif) ,
,.files/image252.gif) ,设墙对A的支持力为
,设墙对A的支持力为.files/image254.gif) 。若保持A的质量
。若保持A的质量.files/image074.gif) 不变,而将A改用密度稍小的材料制作,则A的半径增大,
不变,而将A改用密度稍小的材料制作,则A的半径增大,.files/image257.gif) 角减小,
角减小,.files/image259.gif) 增大,C正确;(
增大,C正确;(.files/image153.gif) 减小,
减小,.files/image262.gif) 减小,
减小,.files/image264.gif) 减小,)。 若保持B的质量
减小,)。 若保持B的质量.files/image077.gif) 不变,而将B改用密度较小的材料制作,则B的半径增大,
不变,而将B改用密度较小的材料制作,则B的半径增大,.files/image257.gif) 增大,
增大,.files/image259.gif) 减小,
减小,.files/image153.gif) 不变,
不变,.files/image268.gif) 不变,
不变,.files/image264.gif) 增大,D正确。
增大,D正确。
.files/image270.gif) 7.B 解析: O点第一次达到正方向最大位移所需时间为
7.B 解析: O点第一次达到正方向最大位移所需时间为.files/image272.gif) ,因此波向前传播的距离为
,因此波向前传播的距离为.files/image274.gif) ,即OP、OP’为
,即OP、OP’为.files/image274.gif) ,因此P、P’两点间距离为半个波长,但由于波是以O为波源向左右传播的,左右对称点振动总相同如图
,因此P、P’两点间距离为半个波长,但由于波是以O为波源向左右传播的,左右对称点振动总相同如图.files/image277.gif) ,因此O点振动时间为
,因此O点振动时间为.files/image279.gif) ,所走路程为
,所走路程为.files/image281.gif) cm,B正确;波动传播的是振动的运动形式,质点并不沿传播方向向前传播,C错;同种波在同一介质中传播的速度是相同的,即
cm,B正确;波动传播的是振动的运动形式,质点并不沿传播方向向前传播,C错;同种波在同一介质中传播的速度是相同的,即.files/image283.gif) ,当O质点振动周期减为2s,则O第一次达到正方向最大位移的时间为0.5s,波向左、右传播的距离为
,当O质点振动周期减为2s,则O第一次达到正方向最大位移的时间为0.5s,波向左、右传播的距离为.files/image285.gif) ,P点还没有振动,D错.
,P点还没有振动,D错.
8.BD 9.D 10.A
11.AD 解析:AD两图中,当滑动变阻器的滑动触头放在最左端时,电源被短路而烧坏;BC两图中,供电电路正确,B图虽然电流表和电压表接错位置,但由于串联的电压表内阻较大,不会烧坏电流表;C图则可测较大电阻的阻值。
12.(1)作图法 ;(2)画出.files/image287.gif) 的s-t图(如图线甲)和
的s-t图(如图线甲)和.files/image100.gif) 的s-t图(如图线乙)
的s-t图(如图线乙)
.files/image290.jpg) 在误差允许的范围内,图线甲为直线,物体从A到B的运动为匀速直线运动,从图线的斜率可求得:
在误差允许的范围内,图线甲为直线,物体从A到B的运动为匀速直线运动,从图线的斜率可求得:.files/image292.gif) ,
,
.files/image294.gif)
从乙图中无法直接判断s、t之间的关系,但是该图线接近于二次函数的图像。为了验证这个猜想,通过转换变量来进行,即作s-t2图线,为此求得表格如下:
.files/image100.gif)
时间t(s)
0.89
1.24
1.52
1.76
1.97
新变量t2(s2)
0.79
1.54
2.31
3.10
3.88
位移s(m)
0.25
0.50
0.75
1.00
1.25
依据上表中的t2、、s数据可作图线丙。从图像中看出s与t2、呈线性变化关系,由图中斜率求得,即.files/image297.gif) 故
故.files/image299.gif)
(3)从.files/image287.gif) 的过程中s随t变化的规律是:
物体作匀速直线运动,
的过程中s随t变化的规律是:
物体作匀速直线运动,.files/image294.gif)
从.files/image100.gif) 的过程中s随t变化的规律是:物体作初速度为零的匀加速直线运动,
的过程中s随t变化的规律是:物体作初速度为零的匀加速直线运动,.files/image304.gif)
13.解析:对质子火箭发动机,加速每一个质子的过程
.files/image306.gif) ①
①
对任意一段时间.files/image308.gif) 内通过质子的总电荷量为q,总质量为M,由能量关系:
内通过质子的总电荷量为q,总质量为M,由能量关系:
.files/image310.gif) ②
②
由动量定理得 .files/image312.gif) ③
③
联立①②③解得
.files/image314.gif) ④
④
14.(1)轮缘转动的线速度:.files/image316.gif) (2分)
(2分)
(2)板运动的加速度:.files/image318.gif) (2分)
(2分)
板在轮子上做匀加速运动的时间:.files/image320.gif) (1分)
(1分)
板在做匀加速运动的全过程中其重心平动发生的位移为:
.files/image322.gif) (1分)
(1分)
板在做匀速运动的全过程中其重心平动发生的位移为:
.files/image324.gif) (1分)
(1分)
因此,板运动的总时间为:.files/image326.gif) (2分)
(2分)
(3)由功能关系知:轮子在传送木板的过程中所消耗 的机械能一部分转化成了木板的动能,另一部分因克服摩擦力做功转化成了内能,即:
木板获得的动能:.files/image328.gif) (1分)
(1分)
摩擦力做功产生的内能:.files/image330.gif) (2分)
(2分)
加速过程木板与轮子间的相对位移:
.files/image332.gif) (1分)
(1分)
消耗的机械能:.files/image334.gif) (2分)
(2分)
联立上述四个方程解得:
.files/image336.gif) (1分)
(1分)
15.解析:⑴正、负电子均经过.files/image124.gif) 次加速后才从加速器射出,故
次加速后才从加速器射出,故
.files/image339.gif) ①
①
.files/image341.gif) ②
②
⑵.files/image031.gif) 时刻
时刻.files/image344.gif) 负,在
负,在.files/image346.gif) 之间加速正电子,则
之间加速正电子,则.files/image348.gif) 时刻在
时刻在.files/image346.gif) 之间加速负电子,且正、负电子在加速器中运动的时间相同,因此射出的时间差即为
之间加速负电子,且正、负电子在加速器中运动的时间相同,因此射出的时间差即为.files/image351.gif) ③
③
⑶由于金属圆筒的静电屏蔽作用,筒内场强为零,电子在每个圆筒中都做匀速运动,要使电子每经过两筒缝隙时都能被加速,运动时间应满足.files/image353.gif) ④
④
电子第一次被加速后的速度即通过.files/image355.gif) 时的速度,因此
时的速度,因此
.files/image357.gif) ⑤
⑤
同理可得
.files/image359.gif)
.files/image361.gif)
…………
解得
.files/image363.gif)
16.解析:⑴设导体棒MN下滑的距离为.files/image164.gif) ,导体棒下滑时受三个力如图所示,由牛顿第二定律得
,导体棒下滑时受三个力如图所示,由牛顿第二定律得 .files/image366.gif) ①
①
.files/image368.gif) ②
②
线框.files/image144.gif) 被导体棒MN分成并联的两部分,对MN两端的总电阻为
被导体棒MN分成并联的两部分,对MN两端的总电阻为
.files/image370.gif)
.files/image372.gif) ③
③
将.files/image166.gif) 时速度为
时速度为.files/image168.gif) 代入得
代入得 .files/image376.gif) ④
④
⑵当导体棒的加速度为零时,由①得 .files/image378.gif) ⑤
⑤
由②③代入.files/image170.gif) 得
得 .files/image381.gif) ⑥
⑥
联立⑤⑥得 .files/image383.gif) ⑦
⑦
⑶假设导体棒以速度.files/image172.gif) 匀速运动,虽然磁感应强度方向与区域Ⅰ中相反,但由楞次定律和左手定则可知,安培力仍沿斜面向上,则有
匀速运动,虽然磁感应强度方向与区域Ⅰ中相反,但由楞次定律和左手定则可知,安培力仍沿斜面向上,则有
.files/image386.gif) ⑧
⑧
由于.files/image388.gif) 为常量,因此当
为常量,因此当.files/image390.gif) 时
时.files/image392.gif) 最大,而式中
最大,而式中.files/image394.gif) ,因此当
,因此当.files/image164.gif) 增大时
增大时.files/image392.gif) 减小,若
减小,若.files/image174.gif) 不变,则速度一定减小,要保持速度不变,则由⑦⑧得
不变,则速度一定减小,要保持速度不变,则由⑦⑧得
.files/image399.gif) ⑨
⑨
.files/image401.gif) ⑩
⑩
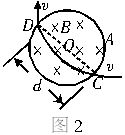
正负电子对撞机的最后部分的简化示意图如图1所示(俯视图),位于水平面内的粗实线所示的圆环形真空管道是正、负电子做圆运动的“容器”,经过加速器加速后的正、负电子分别引入该管道时,具有相等的速度v,它们沿管道向相反的方向运动.在管道内控制它们转弯的是一系列圆形电磁铁,即图中的A1、A2、A3……An,共n个,均匀分布在整个圆环上(图中只示意性地用细实线画了几个),每个电磁铁内的磁场都是匀强磁场,并且磁感应强度都相同,方向竖直向下.磁场区域的直径为d,改变电磁铁内电流的大小,就可改变磁感应强度,从而改变电子偏转角度的大小.经过精确的调整,首先实现了电子沿管道的粗虚线运动,这时电子经每个磁场区域时入射点和出射点都是磁场区域的同一直径的两端,如图2所示.这就为正、负电子的对撞做好了准备.
(1)试确定正、负电子在管道中是沿什么方向旋转的;
(2)已知正、负电子的质量都是m,所带的电荷量都是e,重力不计.求电磁铁内匀强磁场的磁感应强度的大小.


(1)电子刚进入金属极板A、B间时的初速度;
(2)要使所有的电子都能打在荧光屏上,图乙中电压的最大值U0应满足什么条件?
(3)若已知U0且满足(2)中的条件,要使荧光屏上能显示一个完整的波形,荧光屏必须每隔多长时间回到初始位置?计算这个波形的峰值和长度,并在图丙中画出这个波形. 查看习题详情和答案>>
(1)磁感应强度的方向和大小;
(2)在适当的时候,在y轴右方再加一个匀强电场就可使质子最终能沿y轴正方向作匀速直线运动,从质子经过P点开始计时,再经多长时间加这个匀强电场?并求出这个电场的电场强度大小和方向.
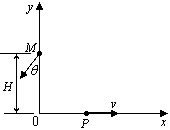
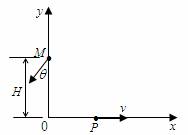
如图所示,在x≥0区域内有垂直于纸面的匀强磁场,一个质量为m、电量为q的质子以速度v水平向右通过x轴上的P点,最后从y轴上M点射出. 已知M点到原点O的距离为H,质子射出磁场时速度方向与y轴负方向夹角θ=30°. 求:
(1)磁感应强度的方向和大小;
(2)在适当的时候,在y轴右方再加一个匀强电场就可使质子最终能沿y轴正方向作匀速直线运动,从质子经过P点开始计时,再经多长时间加这个匀强电场?并求出这个电场的电场强度大小和方向.
(16分)A、B是在真空中水平正对的两块金属板,板长L=40cm,板间距d=24cm,在B板左侧边缘有一粒子源,能连续均匀发射带负电的粒子,粒子紧贴B板水平向右射入,如图甲所示,带电粒子的比荷为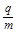 =1.0×108C/kg,初速度v0=2×105m/s(粒子重力不计),在A、B两板间加上如图乙所示的电压,电压的周期T=2.0×10-6s,t=0时刻A板电势高于B板电势,两板间电场可视为匀强电场,电势差U0=360V,A、B板右侧相距s=2cm处有一边界MN,在边界右侧存在一垂直纸面向里的匀强磁场,磁感应强度B=
=1.0×108C/kg,初速度v0=2×105m/s(粒子重力不计),在A、B两板间加上如图乙所示的电压,电压的周期T=2.0×10-6s,t=0时刻A板电势高于B板电势,两板间电场可视为匀强电场,电势差U0=360V,A、B板右侧相距s=2cm处有一边界MN,在边界右侧存在一垂直纸面向里的匀强磁场,磁感应强度B=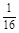 T,磁场中放置一“>”型荧光板,位置如图所示,板与水平方向夹角θ=37°,不考虑粒子之间相互作用及粒子二次进入磁场的可能,求:
T,磁场中放置一“>”型荧光板,位置如图所示,板与水平方向夹角θ=37°,不考虑粒子之间相互作用及粒子二次进入磁场的可能,求: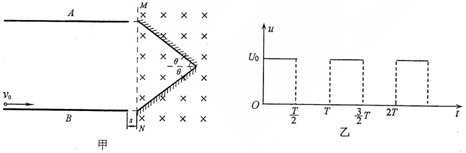
⑴带电粒子在AB间偏转的最大侧向位移ymax;
⑵带电粒子从电场中射出到MN边界上的宽度Δy;
⑶经过足够长时间后,射到荧光板上的粒子数占进入磁场粒子总数的百分比k。