摘要:26.解:(Ⅰ)函数的图象关于原点对称.∴b=0. ------∴.由.且解得∴. ------(Ⅱ)过A.B的切线斜率分别是若.则∴由于(等号当且仅当两数至少一个为零时取得).而(等号当且仅当两数一个为1另一个为-1时取得). 故不可能相等.∴过A点的切线不能与过B点的切线垂直.------(Ⅲ)解法一:当时.切线斜率.∴. 过.的割线的斜率的绝对值恰为.故.------------解法二: ∵.∴.又因为. ∴成立.---点评:本题将导数知识与曲线的切线等几何因素以及不等式等相关知识有机地结合在一起.反映了高中数学的综合性和交汇性.考查了学生综合运用知识的能力.
网址:http://m.1010jiajiao.com/timu_id_4029[举报]
.(本小题满分16分)
函数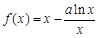 ,其中
,其中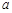 为常数.
为常数.
(1)证明:对任意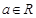 ,函数
,函数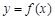 图像恒过定点;
图像恒过定点;
(2)当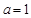 时,不等式
时,不等式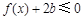 在
在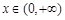 上有解,求实数
上有解,求实数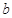 的取值范围;
的取值范围;
(3)若对任意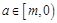 时,函数
时,函数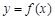 在定义域上恒单调递增,求
在定义域上恒单调递增,求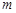 的最小值.
的最小值.
查看习题详情和答案>>
(本题满分16分,第(1)小题4分,第(2)小题6分,第(2)小题6分)
在平行四边形![]() 中,已知过点
中,已知过点![]() 的直线与线段
的直线与线段![]() 分别相交于点
分别相交于点![]() 。若
。若![]() 。
。
(1)求证:![]() 与
与![]() 的关系为
的关系为![]() ;
;
(2)设![]() ,定义在
,定义在![]() 上的偶函数
上的偶函数![]() ,当
,当![]() 时
时![]() ,且函数
,且函数![]() 图象关于直线
图象关于直线![]() 对称,求证:
对称,求证:![]() ,
,![]() 并求
并求![]() 时的解析式;
时的解析式;![]()
(3)在(2)的条件下,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围。
的取值范围。
(本题满分16分,第(1)小题4分,第(2)小题6分,第(2)小题6分)
在平行四边形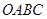 中,已知过点
中,已知过点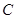 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若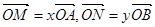 。
。
(1)求证: 与
与 的关系为
的关系为 ;
;
(2)设 ,定义在
,定义在 上的偶函数
上的偶函数 ,当
,当 时
时 ,且函数
,且函数 图象关于直线
图象关于直线 对称,求证:
对称,求证: ,并求
,并求 时的解析式;
时的解析式;
(3)在(2)的条件下,不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围。
的取值范围。
查看习题详情和答案>>
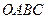 中,已知过点
中,已知过点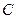 的直线与线段
的直线与线段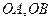 分别相交于点
分别相交于点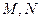 。若
。若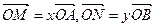 。
。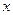 与
与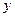 的关系为
的关系为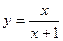 ;
;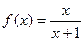 ,定义在
,定义在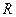 上的偶函数
上的偶函数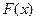 ,当
,当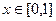 时
时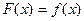 ,且函数
,且函数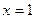 对称,求证:
对称,求证: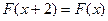 ,
, 并求
并求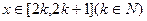 时的解析式;
时的解析式;
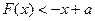 在
在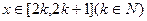 上恒成立,求实数
上恒成立,求实数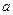 的取值范围。
的取值范围。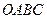 中,已知过点
中,已知过点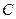 的直线与线段
的直线与线段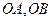 分别相交于点
分别相交于点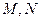 。若
。若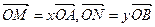 。
。 与
与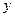 的关系为
的关系为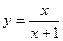 ;
;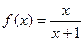 ,定义在
,定义在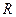 上的偶函数
上的偶函数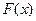 ,当
,当 时
时 ,且函数
,且函数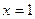 对称,求证:
对称,求证: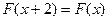 ,
, 并求
并求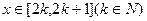 时的解析式;
时的解析式;
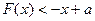 在
在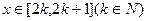 上恒成立,求实数
上恒成立,求实数 的取值范围。
的取值范围。