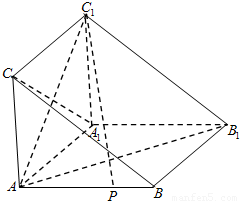
摘要:18.解(1)∵三棱柱ABC―A1B1C1中A1B1是A1C与B1C1的公垂线段.A1C1⊥B1C1AB⊥BC.AB⊥A1C又A1C∩A1B=A1 ∴AB⊥平面A1BC-------4分 (2)∵AB平面ABC.AB⊥平面A1BC ∴面ABC⊥面A1BC作A1O⊥BC垂足为O.则A1O⊥平面ABC -------------- 6分 ∠A1BC为A1B与平面ABC所成角即∠A1BC=60° 在Rt△A1AB中.A1B= 即A1到平面ABC的距离为 -----------------9分 (3) 由O引垂线OH⊥AC垂足为H.连接A1H由三垂线定理可证AC⊥A1H ∴∠A1HO为二面角A1―AC―B平面角 ---------11分 在△ABC中解得OH=.在△OA1H中解得 ∴二面角A1―AC―B大小为 ------14分
网址:http://m.1010jiajiao.com/timu_id_3981[举报]
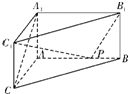 (2012•蓝山县模拟)如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥AC,AC=AA1=1,P为线段AB上的动点.
(2012•蓝山县模拟)如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥AC,AC=AA1=1,P为线段AB上的动点.(1)求证:CA1⊥C1P;
(2)当AP为何值时,二面角C1-PB1-A1的大小为
| π | 6 |
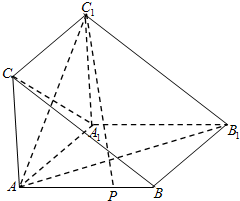 如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC⊥AB,AC=AA1=1,P为线段AB上的动点.
如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC⊥AB,AC=AA1=1,P为线段AB上的动点.(1)求证:CA1⊥C1P;
(2)求CA1与平面AB1C1所成的角的正弦值. 查看习题详情和答案>>
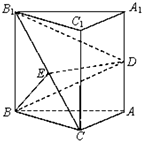 如图,在棱长都等于1的三棱柱ABC-A1B1C1中,BB1⊥平面ABC,D、E分别为AA1、B1C的中点.
如图,在棱长都等于1的三棱柱ABC-A1B1C1中,BB1⊥平面ABC,D、E分别为AA1、B1C的中点.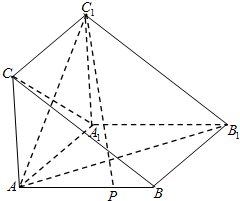 如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC⊥AB,AC=AA1=1,P为线段AB上的动点.
如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC⊥AB,AC=AA1=1,P为线段AB上的动点.