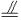题目内容
 如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC⊥AB,AC=AA1=1,P为线段AB上的动点.
如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC⊥AB,AC=AA1=1,P为线段AB上的动点.(1)求证:CA1⊥C1P;
(2)求CA1与平面AB1C1所成的角的正弦值.
分析:(1)由已知中侧棱AA1⊥底面ABC,AC⊥AB,AC=AA1=1,结合直三棱锥的性质及正方形的性质,可得AP⊥CA1,CA1⊥AC1,由线面垂直的判定定理可得CA1⊥平面AC1P,再由线面垂直的性质,可得CA1⊥C1P
(2)由已知中三棱柱ABC-A1B1C1体积为1,可得AB=2,以AA1,A1B1,A1C1分别为x轴、y轴、z轴建立空间直角坐标系,分别求出平面AB1C1的法向量和直线CA1的方向向量,代入向量夹角公式,即可得到CA1与平面AB1C1所成的角的正弦值.
(2)由已知中三棱柱ABC-A1B1C1体积为1,可得AB=2,以AA1,A1B1,A1C1分别为x轴、y轴、z轴建立空间直角坐标系,分别求出平面AB1C1的法向量和直线CA1的方向向量,代入向量夹角公式,即可得到CA1与平面AB1C1所成的角的正弦值.
解答:证明:(1)∵侧棱AA1⊥底面ABC
AA1⊥AB,又AC⊥AB,
∴AB⊥平面AA1C1C,即AP⊥平面AA1C1C,
∴AP⊥CA1,又AC=AA1=1,所以四边形AA1C1C是正方形,
∴CA1⊥AC1,从而CA1⊥平面AC1P,
又C1P?平面AC1P
∴CA1⊥C1P
解:(2)因为三棱柱ABC-A1B1C1体积为1,即V=S△ABC×AA1=
AB×1×1=1,
∴AB=2、
以AA1,A1B1,A1C1分别为x轴、y轴、z轴建立空间直角坐标系,则由题设条件得
A(1,0,0),B1(0,2,0),C1(0,0,1),C(1,0,1),
=(1,0,-1),
=(1,-2,0),设平面AB1C1的法向量
=(x,y,z),则
,
令x=1,则平面AB1C1的法向量
=(1,
,1),又
=(1,0,-1),
所以cos<
•
>=
,
即CA1与平面AB1C1所成的角的正弦值为
AA1⊥AB,又AC⊥AB,
∴AB⊥平面AA1C1C,即AP⊥平面AA1C1C,
∴AP⊥CA1,又AC=AA1=1,所以四边形AA1C1C是正方形,
∴CA1⊥AC1,从而CA1⊥平面AC1P,
又C1P?平面AC1P
∴CA1⊥C1P
解:(2)因为三棱柱ABC-A1B1C1体积为1,即V=S△ABC×AA1=
| 1 |
| 2 |
∴AB=2、
以AA1,A1B1,A1C1分别为x轴、y轴、z轴建立空间直角坐标系,则由题设条件得
A(1,0,0),B1(0,2,0),C1(0,0,1),C(1,0,1),
| C1A |
| B1A |
| n |
|
令x=1,则平面AB1C1的法向量
| n |
| 1 |
| 2 |
| C1A |
所以cos<
| n |
| C1A |
2
| ||
| 3 |
即CA1与平面AB1C1所成的角的正弦值为
2
| ||
| 3 |
点评:本题考查的知识点是直线与平面所成的角,直线与平面垂直的判定与性质,其中(1)的关键是熟练掌握空间直线与直线,直线与平面垂直的相互转化,(2)的关键是建立坐标系,求出直线的方向向量和平面的法向量,将线面夹角问题转化为空间向量夹角问题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
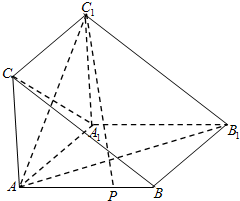
 如图,在体积为1的三棱锥A-BCD侧棱AB、AC、AD上分别取点E、F、G,使AE:EB=AF:FC=AG:GD=2:1,记O为三平面BCG、CDE、DBF的交点,则三棱锥O-BCD的体积等于( )
如图,在体积为1的三棱锥A-BCD侧棱AB、AC、AD上分别取点E、F、G,使AE:EB=AF:FC=AG:GD=2:1,记O为三平面BCG、CDE、DBF的交点,则三棱锥O-BCD的体积等于( ) (2012•蓝山县模拟)如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥AC,AC=AA1=1,P为线段AB上的动点.
(2012•蓝山县模拟)如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥AC,AC=AA1=1,P为线段AB上的动点.