摘要:于是19k2-1<0.
网址:http://m.1010jiajiao.com/timu_id_39614[举报]
(2013•温州二模)己知数列{an}的前n项和为Sn,a1=2.当n≥2时.Sn-1+l,an.Sn+1成等差数列.
(I)求证:{Sn+1}是等比数列:
(II)求数列{nan}的前n项和.
查看习题详情和答案>>
(I)求证:{Sn+1}是等比数列:
(II)求数列{nan}的前n项和.
已知数列{αn}的前n项和为Sn,α1=l,Sn=(2n-1)αn(n∈N*).
(1)证明:数列{αn}是等比数列;
(2)记Tn=n×α1+(n-1)α2+(n-2)α3+…+2×αn-1+1×αn(n∈N*),求L;
(3)证明:当n≥2(n∈N*)时,(1+α1)(1+α2)×…×(1+αn)≤6(1-2αn+1).
查看习题详情和答案>>
(1)证明:数列{αn}是等比数列;
(2)记Tn=n×α1+(n-1)α2+(n-2)α3+…+2×αn-1+1×αn(n∈N*),求L;
(3)证明:当n≥2(n∈N*)时,(1+α1)(1+α2)×…×(1+αn)≤6(1-2αn+1).
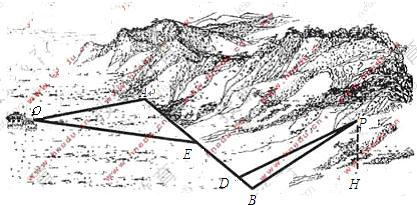
如图,某地为了开发旅游资源,欲修建一条连接风景点P和居民区O的公路,点P所在的山坡面与山脚所在水平面α所成的二面角为θ(0°<θ<90°),且sinθ=
,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用、从点O到山脚修路的造价为a万元/km,原有公路改建费用为
万元/km、当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元、已知OA⊥AB,PB⊥AB,AB=1.5(km),OA=
(km).
(Ⅰ)在AB上求一点D,使沿折线PDAO修建公路的总造价最小;
(Ⅱ)对于(I)中得到的点D,在DA上求一点E,使沿折线PDEO修建公路的总造价最小.
(Ⅲ)在AB上是否存在两个不同的点D′,E′,使沿折线PD′E′O修建公路的总造价小于(Ⅱ)中得到的最小总造价,证明你的结论、
 查看习题详情和答案>>
查看习题详情和答案>>
| 2 |
| 5 |
| a |
| 2 |
| 3 |
(Ⅰ)在AB上求一点D,使沿折线PDAO修建公路的总造价最小;
(Ⅱ)对于(I)中得到的点D,在DA上求一点E,使沿折线PDEO修建公路的总造价最小.
(Ⅲ)在AB上是否存在两个不同的点D′,E′,使沿折线PD′E′O修建公路的总造价小于(Ⅱ)中得到的最小总造价,证明你的结论、
 查看习题详情和答案>>
查看习题详情和答案>>