摘要:18.(1)证明:∵ PA⊥AD.二面角P-AD-C是直二面角.∴ PA⊥面ABCD.∴ PA⊥CD.如图.连接AC.∵ ABCD是菱形.∠BAD=120º.∴ ∠CAD=60º.∠ADC=60º.∴ △ADC是等腰三角形.∵ E是CD的中点.∴ AE⊥CD.∴ CD⊥面PAE.∴ 平面PAE⊥面PCD. --------------------4分(2)如图以A为原点.建立空间直角坐标系A-xyz.∵ PA⊥面ABCD.∴ ∠PCA是PC与面ABCD所成角.∴ ∠PCA=45º.
网址:http://m.1010jiajiao.com/timu_id_39547[举报]
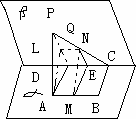
 如图,P-AD-C是直二面角,四边形ABCD是∠BAD=120°的菱形,AB=2,PA⊥AD,E是CD的中点,设PC与平面ABCD所成的角为45°.
如图,P-AD-C是直二面角,四边形ABCD是∠BAD=120°的菱形,AB=2,PA⊥AD,E是CD的中点,设PC与平面ABCD所成的角为45°.(1)求证:平面PAE⊥平面PCD;
(2)试问在线段AB(不包括端点)上是否存在一点F,使得二面角A-PE-D的大小为450?若存在,请求出AF的长,若不存在,请说明理由.
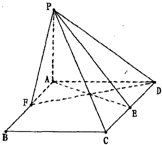 如图,P-AD-C是直二面角,四边形ABCD是∠BAD=120°的菱形,AB=2,PA⊥AD,E是CD的中点,设PC与平面ABCD所成的角为45°.
如图,P-AD-C是直二面角,四边形ABCD是∠BAD=120°的菱形,AB=2,PA⊥AD,E是CD的中点,设PC与平面ABCD所成的角为45°.
(1)求证:平面PAE⊥平面PCD;
(2)试问在线段AB(不包括端点)上是否存在一点F,使得二面角A-PE-D的大小为450?若存在,请求出AF的长,若不存在,请说明理由.
查看习题详情和答案>>
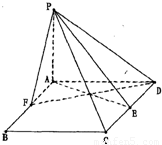
如图,P-AD-C是直二面角,四边形ABCD是∠BAD=120°的菱形,AB=2,PA⊥AD,E是CD的中点,设PC与平面ABCD所成的角为45°.
(1)求证:平面PAE⊥平面PCD;
(2)试问在线段AB(不包括端点)上是否存在一点F,使得二面角A-PE-D的大小为45?若存在,请求出AF的长,若不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求证:平面PAE⊥平面PCD;
(2)试问在线段AB(不包括端点)上是否存在一点F,使得二面角A-PE-D的大小为45?若存在,请求出AF的长,若不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
 ⑴ 求二面角α- l-β的大小
⑴ 求二面角α- l-β的大小