摘要：(I)解:的两个实根.
网址：http://m.1010jiajiao.com/timu_id_390887[举报]
已知定义在R上的函数f（x）=
（sinωx+acosωx）（a∈R，0＜ω≤1）满足：f（x）=f（
-x），f（x-π）=f（x+π）．
（I）求f（x）的解析式；
（II）若m2-4n＞0，m，n∈R，求证：“|m|+|n|＜1”是“方程[f（x）]2+mf（x）+n=0在区间（-
，
）内有两个不等的实根”的充分不必要条件．
查看习题详情和答案>>
已知定义在R上的函数f（x）=
（sinωx+acosωx）（a∈R，0＜ω≤1）满足：f（x）=f（
-x），f（x-π）=f（x+π）．
（I）求f（x）的解析式；
（II）若m2-4n＞0，m，n∈R，求证：“|m|+|n|＜1”是“方程[f（x）]2+mf（x）+n=0在区间（-
，
）内有两个不等的实根”的充分不必要条件．
查看习题详情和答案>>
| 1 |
| 2 |
| π |
| 3 |
（I）求f（x）的解析式；
（II）若m2-4n＞0，m，n∈R，求证：“|m|+|n|＜1”是“方程[f（x）]2+mf（x）+n=0在区间（-
| 5π |
| 6 |
| π |
| 6 |
已知定义在R上的函数f（x）=
（sinωx+acosωx）（a∈R，0＜ω≤1）满足：f（x）=f（
-x），f（x-π）=f（x+π）．
（I）求f（x）的解析式；
（II）若m2-4n＞0，m，n∈R，求证：“|m|+|n|＜1”是“方程[f（x）]2+mf（x）+n=0在区间（-
，
）内有两个不等的实根”的充分不必要条件．
查看习题详情和答案>>
| 1 |
| 2 |
| π |
| 3 |
（I）求f（x）的解析式；
（II）若m2-4n＞0，m，n∈R，求证：“|m|+|n|＜1”是“方程[f（x）]2+mf（x）+n=0在区间（-
| 5π |
| 6 |
| π |
| 6 |
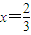时，y=f（x）有极值，求函数f（x）的解析式；
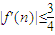？说明理由．
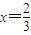时，y=f（x）有极值，求函数f（x）的解析式；
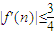？说明理由．