题目内容
已知函数f(x)=+ax2+bx+5,记f(x)的导数为f′(x).(I)若曲线f(x)在点(1,f(1))处的切线斜率为3,且
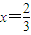 时,y=f(x)有极值,求函数f(x)的解析式;
时,y=f(x)有极值,求函数f(x)的解析式;(II)在(I)的条件下,求函数f(x)在[-4,1]上的最大值和最小值;
(III)若关于x的方程f’(x)=0的两个实数根为α、β,且1<α<β<2试问:是否存在正整数n,使得
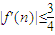 ?说明理由.
?说明理由.
【答案】分析:(I)求出导函数,利用导数在切点处的值为切线斜率及导数在极值点处的值为0,列出方程组,求出a,b.
(II)将a,b的值代入导函数,令导函数为0求出根,列出x,f′(x),f(x)的变化情况的表格,求出最值;
(III)先将二次方程用α,β表示出f(x),利用二次方程的实根分布得到f'(1)>0,f'(2)>0,利用基本不等式求出f′(1)•f′(2)的范围,判断出f′(1),f′(2)的范围.
解答:解:f'(x)=3x2+2ax+b(2分)
(I)由题意,得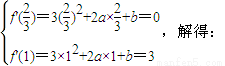
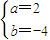
所以,f(x)=x3+2x2-4x+5(4分)
(II)由(I)知,f'(x)=3x2+4x-4=(x+2)(3x-2),
令f'(x)=0,得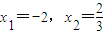
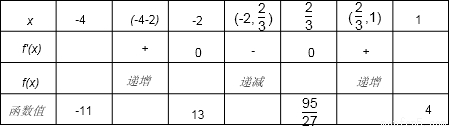
∴f(x)在[-4,1]上的最大值为13,最小值为-11.(10分)
(III)∵f'(x)=3(x-α)(x-β),∴f'(1)>0,f'(2)>0
f'(1)?f'(2)=9(1-α)(1-β)(2-α)(2-β)
=9(α-1)(β-1)(2-α)(2-β)=9(α-1)(2-α)(β-1)(2-β)
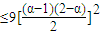
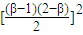 =
=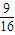
∴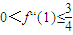 或
或 ,所以存在n1=1或2,使
,所以存在n1=1或2,使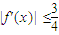 .
.
点评:本题考查导数在极值点处的值是0、考查导数在切点处的值是切线的斜率、考查利用导数求函数的最值的步骤、考查二次方程的实根分布、考查基本不等式.
(II)将a,b的值代入导函数,令导函数为0求出根,列出x,f′(x),f(x)的变化情况的表格,求出最值;
(III)先将二次方程用α,β表示出f(x),利用二次方程的实根分布得到f'(1)>0,f'(2)>0,利用基本不等式求出f′(1)•f′(2)的范围,判断出f′(1),f′(2)的范围.
解答:解:f'(x)=3x2+2ax+b(2分)
(I)由题意,得
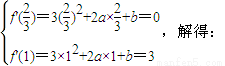
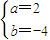
所以,f(x)=x3+2x2-4x+5(4分)
(II)由(I)知,f'(x)=3x2+4x-4=(x+2)(3x-2),
令f'(x)=0,得
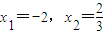

∴f(x)在[-4,1]上的最大值为13,最小值为-11.(10分)
(III)∵f'(x)=3(x-α)(x-β),∴f'(1)>0,f'(2)>0
f'(1)?f'(2)=9(1-α)(1-β)(2-α)(2-β)
=9(α-1)(β-1)(2-α)(2-β)=9(α-1)(2-α)(β-1)(2-β)
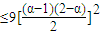
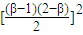 =
=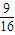
∴
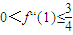 或
或 ,所以存在n1=1或2,使
,所以存在n1=1或2,使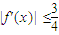 .
.点评:本题考查导数在极值点处的值是0、考查导数在切点处的值是切线的斜率、考查利用导数求函数的最值的步骤、考查二次方程的实根分布、考查基本不等式.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|