摘要:因为.要使函数与函数有且仅有2个不同的交点.则函数的图象与轴的正半轴有且只有两个不同的交点
网址:http://m.1010jiajiao.com/timu_id_390800[举报]
有下列4个命题:
①函数y=f(x)在一点的导数值为0是函数y=f(x)在这点取极值的充要条件;
②若椭圆x2+my2=1的离心率为
,则它的长半轴长为1;
③对于R上可导的任意函数f(x),若满足(x-1)f′(x)≥0,则必有f(0)+f(2)≥2f(1);
④经过点(1,1)的直线,必与
+
=1有2个不同的交点.
其中真命题的为
查看习题详情和答案>>
①函数y=f(x)在一点的导数值为0是函数y=f(x)在这点取极值的充要条件;
②若椭圆x2+my2=1的离心率为
| ||
| 2 |
③对于R上可导的任意函数f(x),若满足(x-1)f′(x)≥0,则必有f(0)+f(2)≥2f(1);
④经过点(1,1)的直线,必与
| x2 |
| 4 |
| y2 |
| 2 |
其中真命题的为
③④
③④
将你认为是真命题的序号都填上)有下列4个命题:
①函数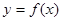 在一点的导数值为
在一点的导数值为 是函数
是函数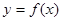 在这点取极值的充要条件;
在这点取极值的充要条件;
②若椭圆 的离心率为
的离心率为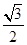 ,则它的长半轴长为1;
,则它的长半轴长为1;
③对于 上可导的任意函数
上可导的任意函数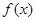 ,若满足
,若满足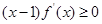 ,则必有
,则必有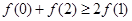
④经过点(1,1)的直线,必与椭圆 有2个不同的交点。
有2个不同的交点。
其中真命题的为 (将你认为是真命题的序号都填上)
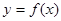 在一点的导数值为
在一点的导数值为 是函数
是函数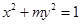 的离心率为
的离心率为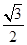 ,则它的长半轴长为1;
,则它的长半轴长为1;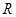 上可导的任意函数
上可导的任意函数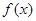 ,若满足
,若满足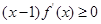 ,则必有
,则必有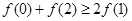
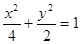 有2个不同的交点。其中真命题的为
有2个不同的交点。其中真命题的为  .
.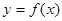 在闭区间
在闭区间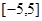 上的大致图像;
上的大致图像;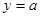 与
与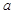 的取值范围.
的取值范围.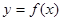 在一点的导数值为
在一点的导数值为 是函数
是函数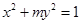 的离心率为
的离心率为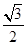 ,则它的长半轴长为1;
,则它的长半轴长为1;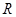 上可导的任意函数
上可导的任意函数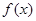 ,若满足
,若满足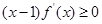 ,则必有
,则必有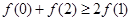
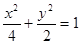 有2个不同的交点。
有2个不同的交点。