题目内容
有下列4个命题:
①、函数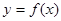 在一点的导数值为
在一点的导数值为 是函数
是函数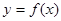 在这点取极值的充要条件;
在这点取极值的充要条件;
②、若椭圆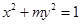 的离心率为
的离心率为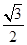 ,则它的长半轴长为1;
,则它的长半轴长为1;
③、对于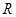 上可导的任意函数
上可导的任意函数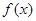 ,若满足
,若满足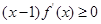 ,则必有
,则必有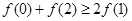
④、经过点(1,1)的直线,必与椭圆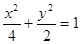 有2个不同的交点。其中真命题的为
有2个不同的交点。其中真命题的为
将你认为是真命题的序号都填上)
【答案】
3,4
【解析】解:因为
命题①、函数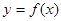 在一点的导数值为
在一点的导数值为 是函数
是函数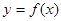 在这点取极值的充要条件;应该是必要不充分条件。
在这点取极值的充要条件;应该是必要不充分条件。
命题②、若椭圆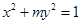 的离心率为
的离心率为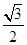 ,则它的长半轴长为1;因为焦点位置不定,因此m有两种情况,因此错误。
,则它的长半轴长为1;因为焦点位置不定,因此m有两种情况,因此错误。
命题③、对于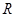 上可导的任意函数
上可导的任意函数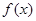 ,若满足
,若满足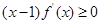 ,则必有
,则必有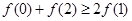 成立
成立
命题④、经过点(1,1)的直线,必与椭圆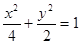 有2个不同的交点,成立。
有2个不同的交点,成立。

练习册系列答案
相关题目