摘要:(III)设是方程的实数根.求证:对于定义域中任意的.
网址:http://m.1010jiajiao.com/timu_id_390661[举报]
设M是由满足下列两个条件的函数![]() 构成的集合:
构成的集合:
①议程![]() 有实根;②函数
有实根;②函数![]() 的导数
的导数![]() 满足0<
满足0<![]() <1.
<1.
(I)若![]() ,判断方程
,判断方程![]() 的根的个数;
的根的个数;
(II)判断(I)中的函数![]() 是否为集合M的元素;
是否为集合M的元素;
(III)对于M中的任意函数![]() ,设x1是方程
,设x1是方程![]() 的实根,求证:对于
的实根,求证:对于![]() 定义域中任意的x2,x3,当| x2-x1|<1,且| x3-x1|<1时,有
定义域中任意的x2,x3,当| x2-x1|<1,且| x3-x1|<1时,有![]()
设M是由满足下列两个条件的函数 构成的集合:
构成的集合:
①议程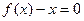 有实根;②函数
有实根;②函数 的导数
的导数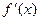 满足0<
满足0<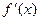 <1.
<1.
(I)若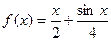 ,判断方程
,判断方程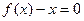 的根的个数;
的根的个数;
(II)判断(I)中的函数 是否为集合M的元素;
是否为集合M的元素;
(III)对于M中的任意函数 ,设x1是方程
,设x1是方程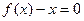 的实根,求证:对于
的实根,求证:对于 定义域中任意的x2,x3,当| x2-x1|<1,且| x3-x1|<1时,有
定义域中任意的x2,x3,当| x2-x1|<1,且| x3-x1|<1时,有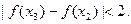
 构成的集合:
构成的集合:①议程
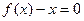 有实根;②函数
有实根;②函数 的导数
的导数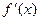 满足0<
满足0<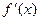 <1.
<1.(I)若
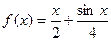 ,判断方程
,判断方程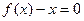 的根的个数;
的根的个数;(II)判断(I)中的函数
 是否为集合M的元素;
是否为集合M的元素;(III)对于M中的任意函数
 ,设x1是方程
,设x1是方程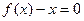 的实根,求证:对于
的实根,求证:对于 定义域中任意的x2,x3,当| x2-x1|<1,且| x3-x1|<1时,有
定义域中任意的x2,x3,当| x2-x1|<1,且| x3-x1|<1时,有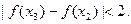
设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]()
![]() 有实数根;②函数
有实数根;②函数![]() 的导数
的导数![]() 满足
满足![]() .”
.”
(I)判断函数![]() 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素![]() 具有下面的性质:若
具有下面的性质:若![]() 的定义域为D,则对于任意
的定义域为D,则对于任意
[m,n]![]() D,都存在
D,都存在![]()
![]() [m,n],使得等式
[m,n],使得等式![]() 成立”,
成立”,
试用这一性质证明:方程![]() 只有一个实数根;
只有一个实数根;
(III)设![]() 是方程
是方程![]() 的实数根,求证:对于
的实数根,求证:对于![]() 定义域中任意的
定义域中任意的![]() .
.
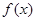 构成的集合:“①方程
构成的集合:“①方程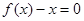 有实数根;②函数
有实数根;②函数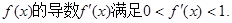 ”
”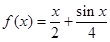 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由; 成立。试用这一性质证明:方程
成立。试用这一性质证明:方程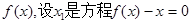 的实数根,求证:对于
的实数根,求证:对于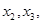 当
当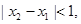 且
且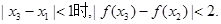
 构成的集合:“①方程
构成的集合:“①方程 有实数
有实数 ”[来源:学+科+网Z+X+X+K]
”[来源:学+科+网Z+X+X+K] 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由; 成立。试用这一性
成立。试用这一性 的实数根,求证:对于
的实数根,求证:对于 当
当 且
且