题目内容
设M是由满足下列两个条件的函数![]() 构成的集合:
构成的集合:
①议程![]() 有实根;②函数
有实根;②函数![]() 的导数
的导数![]() 满足0<
满足0<![]() <1.
<1.
(I)若![]() ,判断方程
,判断方程![]() 的根的个数;
的根的个数;
(II)判断(I)中的函数![]() 是否为集合M的元素;
是否为集合M的元素;
(III)对于M中的任意函数![]() ,设x1是方程
,设x1是方程![]() 的实根,求证:对于
的实根,求证:对于![]() 定义域中任意的x2,x3,当| x2-x1|<1,且| x3-x1|<1时,有
定义域中任意的x2,x3,当| x2-x1|<1,且| x3-x1|<1时,有![]()
(1)唯一 (2)是
解析:
(I)令![]()
则![]()
![]() 是单调递减函数.
是单调递减函数.
又取![]()
![]() 在其定义域上有唯一实根.
在其定义域上有唯一实根.
(II)由(I)知方程![]() 有实根(或者由
有实根(或者由![]() ,易知x=0就是方程的一个根),
,易知x=0就是方程的一个根),![]() 满足条件①.
满足条件①.
![]()
![]() 满足条件②.故
满足条件②.故![]() 是集合M中的元素.
是集合M中的元素.
(III)不妨设![]() 在其定义域上是增函数.
在其定义域上是增函数.
![]()
![]() 是其定义域上的减函数.
是其定义域上的减函数.
![]() .
.
![]()
![]()

练习册系列答案
相关题目
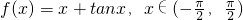 ;
; ;
;