摘要：得
网址：http://m.1010jiajiao.com/timu_id_390648[举报]
已知数列
（I）若函数
求证：
；
（II）设
。试问：是否存在关于n的整式g(n)，使得
对于一切不小于2的自然数n恒成立？若不存在，试说明理由；若存在，写现g(n)的解析式，并加以证明。
已知数列
满足
（I）求数列的通项公式；
（II）若数列
中
，前
项和为
，且
证明：
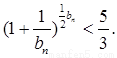
【解析】第一问中，利用
，
∴数列{
}是以首项a1+1，公比为2的等比数列，即
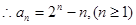
第二问中，
进一步得到得
即
即
是等差数列.
然后结合公式求解。
解：（I） 解法二、，
∴数列{}是以首项a1+1，公比为2的等比数列，即
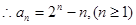
（II） ………②
由②可得：
…………③
③－②，得 即 …………④
又由④可得
…………⑤
⑤－④得
即
是等差数列.
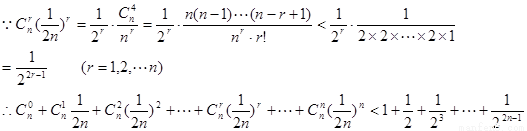
查看习题详情和答案>>
已知函数f（x）=ax2+bx+5，记f（x）的导数为f′（x）．
（I）若曲线f（x）在点（1，f（1））处的切线斜率为3，且x=
时，y=f（x）有极值，求函数f（x）的解析式；
（II）在（I）的条件下，求函数f（x）在[-4，1]上的最大值和最小值；
（III）若关于x的方程f’（x）=0的两个实数根为α、β，且1＜α＜β＜2试问：是否存在正整数n0，使得|f′(n0)|≤
？说明理由．
查看习题详情和答案>>
（I）若曲线f（x）在点（1，f（1））处的切线斜率为3，且x=
| 2 |
| 3 |
（II）在（I）的条件下，求函数f（x）在[-4，1]上的最大值和最小值；
（III）若关于x的方程f’（x）=0的两个实数根为α、β，且1＜α＜β＜2试问：是否存在正整数n0，使得|f′(n0)|≤
| 3 |
| 4 |
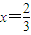时，y=f（x）有极值，求函数f（x）的解析式；
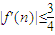？说明理由．
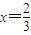时，y=f（x）有极值，求函数f（x）的解析式；
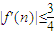？说明理由．