Question

已知数列

   （I）若函数求证：；

   （II）设。试问：是否存在关于n的整式g(n)，使得对于一切不小于2的自然数n恒成立？若不存在，试说明理由；若存在，写现g(n)的解析式，并加以证明。

Answer 1

解：

又是以1为首项，1为公差的等差数列，

                                                        

   （I），

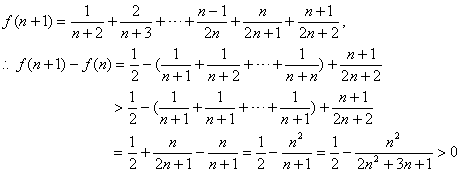
是单调递增的，

故，

                                                                          

   （II）

假设存在关于n的整式满足要求，则有

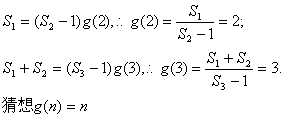
下面用数学归纳法证明：对于一切不小于2的自然数n恒成立。

①当n=2时，左边，

所以左边=右边。

②假设时，等式成立，

即，

则当时，

左边

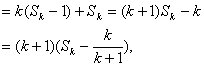
右边

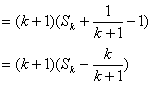
时，等式也成立。

由①、②可知，等式对于一切不小于2的自然数n恒成立。

故存在满足要求的整式 。