摘要:(Ⅲ)若P(x0.y0)为图象上的任意一点.直线l与的图象相切于点P.求直线l的斜率的取值范围.解:(Ⅰ)已知函数.----1分
网址:http://m.1010jiajiao.com/timu_id_390407[举报]
已知函数f(x)=ex-ax(a∈R).
(Ⅰ) 写出函数y=f(x)的图象恒过的定点坐标;
(Ⅱ)直线L为函数y=φ(x)的图象上任意一点P(x0,y0)处的切线(P为切点),如果函数y=φ(x)图象上所有的点(点P除外)总在直线L的同侧,则称函数y=φ(x)为“单侧函数”.
(i)当a= 判断函数y=f(x)是否为“单侧函数”,若是,请加以证明,若不是,请说明理由.
判断函数y=f(x)是否为“单侧函数”,若是,请加以证明,若不是,请说明理由.
(i i)求证:当x∈(-2,+∞)时,ex+ x≥ln(
x≥ln( x+1)+1.
x+1)+1.
查看习题详情和答案>>
已知函数f(x)=ln(2+mx)-
x2.
(1)若f(x)在
处取得极值,求m的值;
(2)若以函数F(x)=f(x)+
x2(x∈(0,3])图象上任意一点P(x0,y0)为切点的切线的斜率k≥
恒成立,求正实数m的最小值;
查看习题详情和答案>>
| 3 |
| 2 |
(1)若f(x)在
| 1 |
| 3 |
(2)若以函数F(x)=f(x)+
| 3 |
| 2 |
| 1 |
| 4 |
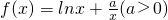
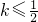 恒成立,求实数a的最小值.
恒成立,求实数a的最小值.