题目内容
已知函数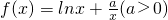
(I)求f(x)的单调区间;
(II)若以y=f(x)(x∈(0,3])图象上任意一点P(x0,y0)为切点的切线的斜率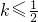 恒成立,求实数a的最小值.
恒成立,求实数a的最小值.
解:(Ⅰ)由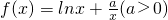 ,得:
,得:
∵函数f(x)的定义域为{x|x>0},且a>0.
∴当x∈(0,a)时,f′(x)<0,
当x∈(a,+∞)时,f′(x)>0.
∴函数f(x)的减区间为(0,a),增区间为(a,+∞).
(Ⅱ)由(Ⅰ)得: ,
,
以y=f(x)(x∈(0,3])图象上任意一点P(x0,y0)为切点的切线的斜率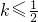 恒成立,
恒成立,
即 对x0∈(0,3]恒成立,即
对x0∈(0,3]恒成立,即 对x0∈(0,3]恒成立,
对x0∈(0,3]恒成立,
也就是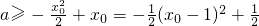 对x0∈(0,3]恒成立,
对x0∈(0,3]恒成立,
令g(x)= (x0∈(0,3]),
(x0∈(0,3]),
当x=1时, ,
,
∴a .
.
∴所求实数a的最小值为 .
.
分析:(Ⅰ)求出原函数的导函数,在函数的定义域内分x∈(0,a)和(a,+∞)讨论导函数的符号,从而得到原函数的单调区间;
(Ⅱ)求出函数在x=x0处的导函数,根据题意以y=f(x)(x∈(0,3])图象上任意一点P(x0,y0)为切点的切线的斜率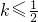 恒成立,可得导函数
恒成立,可得导函数 对x0∈(0,3]恒成立,分离参数后求函数的最大值.
对x0∈(0,3]恒成立,分离参数后求函数的最大值.
点评:本题考查了利用函数的导函数研究函数的单调性,考查了导数的几何意义,函数在图象上某点处的切线的斜率就是在该点处的导数值,考查了利用分离变量法求参数的取值范围,此题是中档题.
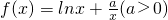 ,得:
,得:
∵函数f(x)的定义域为{x|x>0},且a>0.
∴当x∈(0,a)时,f′(x)<0,
当x∈(a,+∞)时,f′(x)>0.
∴函数f(x)的减区间为(0,a),增区间为(a,+∞).
(Ⅱ)由(Ⅰ)得:
 ,
,以y=f(x)(x∈(0,3])图象上任意一点P(x0,y0)为切点的切线的斜率
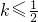 恒成立,
恒成立,即
 对x0∈(0,3]恒成立,即
对x0∈(0,3]恒成立,即 对x0∈(0,3]恒成立,
对x0∈(0,3]恒成立,也就是
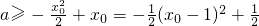 对x0∈(0,3]恒成立,
对x0∈(0,3]恒成立,令g(x)=
 (x0∈(0,3]),
(x0∈(0,3]),当x=1时,
 ,
,∴a
 .
.∴所求实数a的最小值为
 .
.分析:(Ⅰ)求出原函数的导函数,在函数的定义域内分x∈(0,a)和(a,+∞)讨论导函数的符号,从而得到原函数的单调区间;
(Ⅱ)求出函数在x=x0处的导函数,根据题意以y=f(x)(x∈(0,3])图象上任意一点P(x0,y0)为切点的切线的斜率
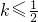 恒成立,可得导函数
恒成立,可得导函数 对x0∈(0,3]恒成立,分离参数后求函数的最大值.
对x0∈(0,3]恒成立,分离参数后求函数的最大值.点评:本题考查了利用函数的导函数研究函数的单调性,考查了导数的几何意义,函数在图象上某点处的切线的斜率就是在该点处的导数值,考查了利用分离变量法求参数的取值范围,此题是中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目

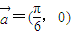 平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的单调区间及值域.
平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的单调区间及值域.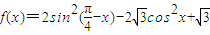
 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.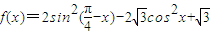
 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.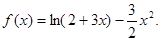
 成立,求实数a的取值范围;
成立,求实数a的取值范围;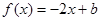 在[0,1]上恰有两个不同的实根,求实数b的取值范围.
在[0,1]上恰有两个不同的实根,求实数b的取值范围.
 恒成立.
恒成立.