摘要：(3)令函数的图象为曲线C2.若存在实数b使得曲线C2在处有斜率为-8的切线.求实数a的取值范围.解:(1)
网址：http://m.1010jiajiao.com/timu_id_390257[举报]
定义函数F（x，y）=（1+x）y，x，y∈（0，+∞）．
（1）令函数f（x）=F[1，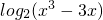
]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程；
（2）令函数g（x）=F[1，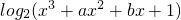
]的图象为曲线C2，若存在实数b使得曲线C2在x0（x0∈（1，4））处有斜率为-8的切线，求实数a的取值范围；
（3）当x，y∈N*，且x＜y时，证明F（x，y）＞F（y，x）．
查看习题详情和答案>>
定义函数F（x，y）=（1+x）y，x，y∈（0，+∞）．
（1）令函数f（x）=F[1，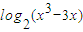
]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程；
（2）令函数g（x）=F[1，
]的图象为曲线C2，若存在实数b使得曲线C2在x（x∈（1，4））处有斜率为-8的切线，求实数a的取值范围；
（3）当x，y∈N*，且x＜y时，证明F（x，y）＞F（y，x）．
查看习题详情和答案>>
（1）令函数f（x）=F[1，
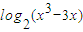]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程；（2）令函数g（x）=F[1，
]的图象为曲线C2，若存在实数b使得曲线C2在x（x∈（1，4））处有斜率为-8的切线，求实数a的取值范围；（3）当x，y∈N*，且x＜y时，证明F（x，y）＞F（y，x）．
查看习题详情和答案>>
定义函数F（x，y）=（1+x）y，x，y∈（0，+∞）．
（1）令函数f（x）=F[1，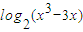
]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程；
（2）令函数g（x）=F[1，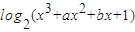
]的图象为曲线C2，若存在实数b使得曲线C2在x（x∈（1，4））处有斜率为-8的切线，求实数a的取值范围；
（3）当x，y∈N*，且x＜y时，证明F（x，y）＞F（y，x）．
查看习题详情和答案>>
（1）令函数f（x）=F[1，
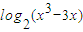]的图象为曲线C1求与直线4x+15y-3=0垂直的曲线C1的切线方程；（2）令函数g（x）=F[1，
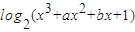]的图象为曲线C2，若存在实数b使得曲线C2在x（x∈（1，4））处有斜率为-8的切线，求实数a的取值范围；（3）当x，y∈N*，且x＜y时，证明F（x，y）＞F（y，x）．
查看习题详情和答案>>