摘要：(Ⅲ)是否存在实数.使得函数的图象与的图象恰好有四个不同的交点?若存在.求出的取值范围.若不存在.说名理由.
网址：http://m.1010jiajiao.com/timu_id_390228[举报]
函数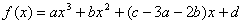
的图像如图所示。
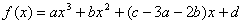的图像如图所示。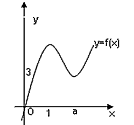 
（1）若函数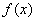
在x=2处的切线方程为
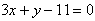，求函数
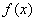的解析式；
（2）在（1）的条件下，是否存在实数m，使得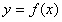
的图像与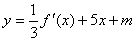
的图像有且只有三个不同的交点？若存在，求出m的取值范围；若不存在，说明理由。
查看习题详情和答案>>
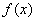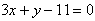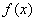在x=2处的切线方程为，求函数的解析式；（2）在（1）的条件下，是否存在实数m，使得
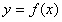的图像与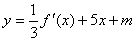的图像有且只有三个不同的交点？若存在，求出m的取值范围；若不存在，说明理由。
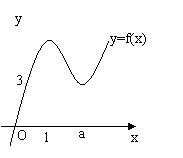
函数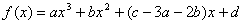
的图像如图所示。
（1）若函数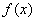
在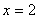
处的切线方程为
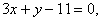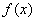求函数的解析式
（2）在（1）的条件下，是否存在实数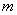
，使得
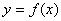的图像与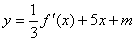
的图像有且只有三个不同的交点？若存在，求出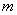的取值范围；若不存在，说明理由。
 |
查看习题详情和答案>>
若存在实数k，b，使得函数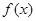
和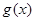
对其定义域上的任意实数x同时满足：
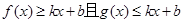，则称直线：
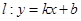为函数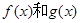
的“隔离直线”。已知
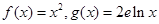（其中e为自然对数的底数）。试问：
（1）函数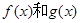的图象是否存在公共点，若存在，求出交点坐标，若不存在，说明理由；
（2）函数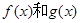是否存在“隔离直线”？若存在，求出此“隔离直线”的方程；若不存在，请说明理由。
查看习题详情和答案>>
函数y=f（x）是定义在R上的偶函数，且f（-1+x）=f（-1-x），当x∈[-2，-1]时，f（x）=t（x+2）3-t（x+2）（t∈R），记函数y=f（x）的图象在（| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
（Ⅰ）求y=f（x）在[0，1]上的解析式；
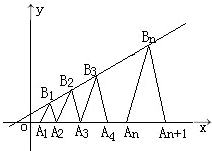
（Ⅱ）点列B1（b1，2），B2（b2，3），…，Bn（bn，n+1）在l上，A1（x1，0），A2（x2，0），…，An（xn，0）依次为x轴上的点，如图，当n∈N*时，点An，Bn，An+1构成以AnAn+1为底边的等腰三角形．若x1=a（0＜a＜1），求数列{xn}的通项公式；
（Ⅲ）在（Ⅱ）的条件下，是否存在实数a使得数列{xn}是等差数列？如果存在，写出a的一个值；如果不存在，请说明理由． 查看习题详情和答案>>