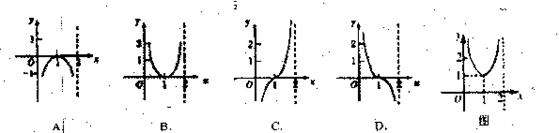题目内容
函数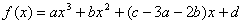 的图像如图所示。
的图像如图所示。
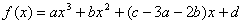 的图像如图所示。
的图像如图所示。 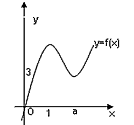
(1)若函数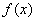 在x=2处的切线方程为
在x=2处的切线方程为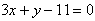 ,求函数
,求函数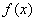 的解析式;
的解析式;
(2)在(1)的条件下,是否存在实数m,使得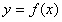 的图像与
的图像与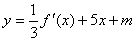 的图像有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,说明理由。
的图像有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,说明理由。
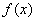 在x=2处的切线方程为
在x=2处的切线方程为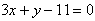 ,求函数
,求函数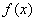 的解析式;
的解析式;(2)在(1)的条件下,是否存在实数m,使得
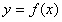 的图像与
的图像与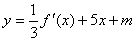 的图像有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,说明理由。
的图像有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,说明理由。 解:(1)由图象可知函数f(x)的图像过点(0,3),且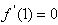 , ,∴ 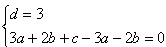 ,解得: ,解得: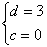 , ,依题意,f′(2)=-3且f(2)=5, 解得:a=1,b=-6, 所以  。 。(2)由题意,可得 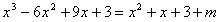 有三个不相等的实根, 有三个不相等的实根,即 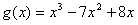 与y=m有三个不同的交点, 与y=m有三个不同的交点,∴ 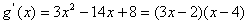 , ,
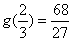 , ,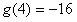 , ,故m的取值范围是 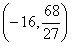 。 。 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
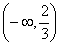
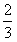
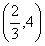
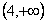
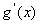
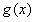
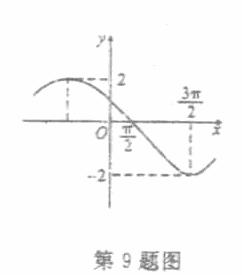
 的图像如图所示,且
的图像如图所示,且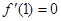 .则
.则 的值是 .
的值是 .
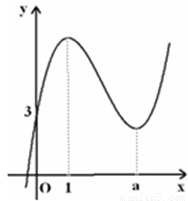
 的图像如图所示,则函数
的图像如图所示,则函数 的图像可能是( )
的图像可能是( )
 的定义域为
的定义域为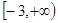 ,
,  ,
, ,
, ,其导函数的图像如图所示,若正数
,其导函数的图像如图所示,若正数 满足
满足 ,则
,则  的取值范围是
的取值范围是 
 B、
B、 C、
C、 D、
D、
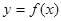 图像如图所示,则函数
图像如图所示,则函数 的图像大致是 ( )
的图像大致是 ( )