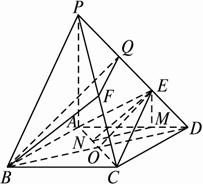
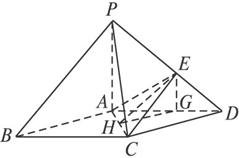
OF2+(PE)2=OE2.令PA=a.则OE=.PO=.PE=.计算得k=1.所以k=1时.O在面PBC内的射影恰好为的重心. 13分——青夏教育精英家教网——

摘要：OF2+(PE)2=OE2.令PA=a.则OE=.PO=.PE=.计算得k=1.所以k=1时.O在面PBC内的射影恰好为的重心. 13分

网址：http://m.1010jiajiao.com/timu_id_38939[举报]

设函数f（x）=px-

-2lnx，且f（e）=pe-

-2，（其中e=2.1828…是自然对数的底数）．
（1）求p与q的关系；
（2）若f（x）在其定义域内为单调函数，求p的取值范围；
（3）设g(x)=

，若在[1，e]上存在实数x₀，使得f（x₀）＞g（x₀）成立，求实数p的取值范围．查看习题详情和答案>>

在平面直角坐标系中，已知向量

=(c，0)(c为常数，且c＞0)，

=(x，x)(x∈R)，|

|的最小值为1，

，t）（a为常数，且a＞c，t∈R）．动点P同时满足下列三个条件：
（1）|

(λ∈R，且λ≠0)；
（2）动点P的轨迹C经过点B（0，-1）．
（Ⅰ）求曲线C的方程；
（Ⅱ）是否存在方向向量为m=（1，k）（k≠0）的直线l，l与曲线C相交于M、N两点，使|

的夹角为60°？若存在，求出k值，并写出直线l的方程；若不存在，请说明理由．查看习题详情和答案>>

（08年岳阳一中二模文）（13分）如图，在底面是菱形的四棱锥P―ABCＤ中，∠ABC=60⁰，PA=AC=a，PB=PD=,点E

在PD上，且PE:ED=2:1。

（1）证明PA⊥平面ABCD；

（2）求以AC为棱，EAC与DAC为面的二面角的大小；

（3）在棱PC上是否存在一点F，使BF//平面AEC？证明你的结论。

查看习题详情和答案>>

底面是菱形的四棱锥P—ABCD中,∠ABC=60°,PA=AC=a,PA⊥平面ABCD,点E在PD上,且PE∶ED=2∶1.

(1)求二面角EACD的?大小?.

(2)在棱PC上是否存在一点F,使BF∥平面AEC?若存在,求出点F;若不存在,请说明理由.

查看习题详情和答案>>

如图，在底面是菱形的四棱锥P—ABCD中，∠ABC=60°，PA=AC=a,PB=PD=a,点E在PD上，且PE∶ED=2∶1.

(1)证明PA⊥平面ABCD；

(2)求以AC为棱，EAC与DAC为面的二面角θ的大小；

(3)在棱PC上是否存在一点F，使BF∥平面AEC？证明你的结论.

查看习题详情和答案>>