网址:http://m.1010jiajiao.com/timu_id_37806[举报]
请尝试解决以下问题:
(1)如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,
由旋转可得:AB="AD,BG=DE," ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45° ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2, ∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
(2)运用(1)解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(AD>BC),∠D=90°,AD=CD=10,E是CD上一点,且∠BAE=45°,DE=4,求BE的长.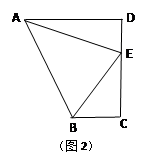
(3)类比(1)证明思想完成下列问题:在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),在旋转过程中,等式BD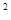 +CE
+CE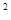 =DE
=DE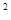 始终成立,请说明理由.
始终成立,请说明理由.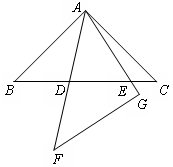
请尝试解决以下问题:
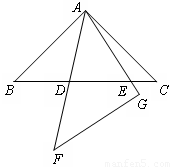
(1)如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,

由旋转可得:AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45° ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2, ∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
(2)运用(1)解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(AD>BC),∠D=90°,AD=CD=10,E是CD上一点,且∠BAE=45°,DE=4,求BE的长.

(2)类比(1)证明思想完成下列问题:在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),在旋转过程中,等式BD +CE
+CE =DE
=DE 始终成立,请说明理由.
始终成立,请说明理由.
查看习题详情和答案>>
已知:在四边形ABCD中,AB=DC,AC=DB,AD≠BC。求证:四边形ABCD是等腰梯形。
下面是某同学证明这道题的过程:
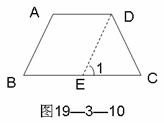
证明:过D作DE∥AB,交BC于E,如图19-3-10所示,则∠ABC=∠1。①
∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB,②
∴∠ABC=∠DCB,③
∴∠1=∠DCB,④
∴AB=DC=DE,⑤
∴四边形ABED是平行四边形,⑥
∴AD∥BC,⑦
BE=AD,⑧
又∵AD≠BC,∴BE≠B,
∴点E,C是不同的点,DC不平行于AB。⑨
∵AB=DC,
∴四边形ABCD是等腰梯形。⑩
阅读后填空:
(1)上面的证明过程是否有错误?如有,错在第几步?答:_________;
(2)作DE∥AB的目的是__________;
(3)有人认为第⑨步是多余的,你认为它是否多余?为什么?_________;
(4)判断四边形ABED是平行四边形的依据为___________;
(5)判断四这形ABCD是等腰梯形的依据为_____________;
(6)若题设中没有AD≠BC,那么四边形ABCD一定是等腰梯形吗?为什么?
答:_________________。
查看习题详情和答案>>分析:可利用∠DCE作为中间量过渡。
解法1 :
∵AB∥CD,∠B=50°,( )
∴∠DCE=∠_______ =_______ °。(____________ ,______)
又∵AD∥BC,( )
∴∠D=∠______ =_______ °。(____________ ,____________)
想一想:如果以∠A作为中间量,如何求解?
解法2 :
∵AD∥BC,∠B=50°,( )
∴∠A+∠B=______ 。(____________ ,____________)
即∠A=______ -______ =______ °-______ °=______ °。
∵DC∥AB,( )
∴∠D+∠A=______ 。(_____________ ,_____________)
即∠D=______ -______ =______ °-______ °=______ °。

 多彩数学,所有三角形都是等腰三角形
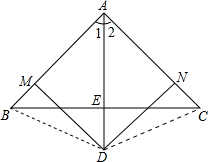
多彩数学,所有三角形都是等腰三角形下面的推理过程,请你指出其错误之处.如图:△ABC中,∠BAC的平分线和BC边的垂直平分线相交于D,过点D作DM⊥AB于M,DN⊥AC于N.求证:AB=AC.
证明:连结BD、CD.
∵DM⊥AB,∴∠DMA=90°.∵DN⊥AC,∴∠AND=90°.∴∠AMD=∠AND=90°.又AD平分∠BAC,∴∠1=∠2.又∵AD=AD,∵△ADM≌△ADN(AAS),∴AM=AN,DM=DN.∵DE垂直平分BC,∴DB=DC.在Rt△BDM与Rt△CDN中,
|
分三种情况:
(1)AB=AC时成立;
(2)AB>AC时,N在AC的延长线上;
(3)AB<AC时,M在AB的延长线上.