题目内容
请尝试解决以下问题:
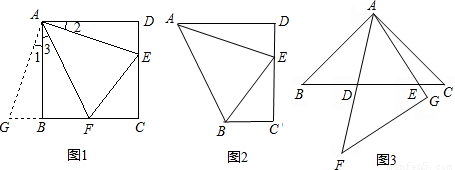
(1)如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,

由旋转可得:AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45° ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2, ∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.
(2)运用(1)解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(AD>BC),∠D=90°,AD=CD=10,E是CD上一点,且∠BAE=45°,DE=4,求BE的长.

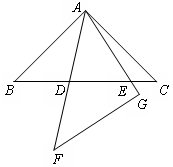
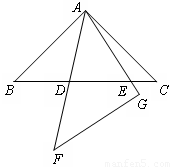
(2)类比(1)证明思想完成下列问题:在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),在旋转过程中,等式BD +CE
+CE =DE
=DE 始终成立,请说明理由.
始终成立,请说明理由.
解:(1)EAF、△EAF、GF
(2) 过A作AG⊥BC,交BC延长线于G.

在直角梯形ABCD中,
∵AD∥BC,∴∠C=∠D=90°,
又∠CGA=90°,AD=CD,
∴四边形AGCD 为正方形.
∴CG=AD=10.
已知∠BAE=45°,
根据(1)可知,BE=GB+DE.
设BE=x,则BG=x-4,
∴BC=14-x.
在Rt△BCE中, ∵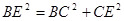 ,即
,即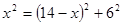 .
.
解这个方程,得:x=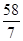 .
.
∴BE=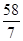 .
.
(3)证明:如下图,将∆ACE绕点A顺时针旋转90°至∆ABH的位置,
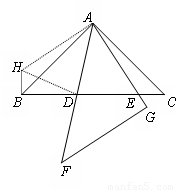
则CE=HB,AE=AH,∠ABH=∠C=45°,旋转角∠EAH=90°.
连接HD,在∆EAD和∆HAD中
∵AE=AH,∠HAD=∠EAH-∠FAG=45°=∠EAD, AD=AD.
∴∆EAD≌∆HAD ∴DH=DE
又∠HBD=∠ABH+∠ABD=90° ∴BD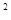 +HB
+HB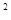 =DH
=DH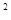
即BD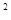 +CE
+CE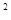 =DE
=DE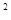
【解析】(1)利用角之间的等量代换得出∠GAF=∠FAE,再利用SAS得出△GAF≌△EAF,得出答案;
(2)过A作AG⊥BC,交BC延长线于G,由正方形的性质得出CG=AD=10,再运用勾股定理和方程求出BE的长;
(3)运用旋转性质和勾股定理判断说明等式成立.



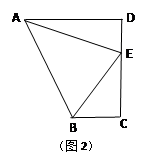
 +CE
+CE