题目内容
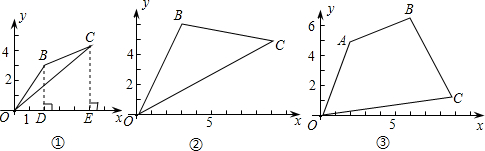
(2007•海淀区二模)例.如图①,平面直角坐标系xOy中有点B(2,3)和C(5,4),求△OBC的面积.
解:过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.依题意,可得
S△OBC=S梯形BDEC+S△OBD-S△OCE
=
(BD+CE)(OE-OD)+
OD•BD-
•OE•CE
=
×(3+4)×(5-2)+
×2×3-
×5×4=3.5.
∴△OBC的面积为3.5.
(1)如图②,若B(x1,y1)、C(x2,y2)均为第一象限的点,O、B、C三点不在同一条直线上.仿照例题的解法,求△OBC的面积(用含x1、x2、y1、y2的代数式表示);
(2)如图③,若三个点的坐标分别为A(2,5),B(7,7),C(9,1),求四边形OABC的面积.
解:过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.依题意,可得
S△OBC=S梯形BDEC+S△OBD-S△OCE
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴△OBC的面积为3.5.
(1)如图②,若B(x1,y1)、C(x2,y2)均为第一象限的点,O、B、C三点不在同一条直线上.仿照例题的解法,求△OBC的面积(用含x1、x2、y1、y2的代数式表示);
(2)如图③,若三个点的坐标分别为A(2,5),B(7,7),C(9,1),求四边形OABC的面积.

分析:(1)过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.根据图形知S△OBC=S梯形BCED+S△OBD-S△OCE;
(2)连接OB.根据图形知S四边形OABC=S△OAB+S△OBC;
利用梯形、三角形的面积公式可以分别求得S△OBC、S四边形OABC.
(2)连接OB.根据图形知S四边形OABC=S△OAB+S△OBC;
利用梯形、三角形的面积公式可以分别求得S△OBC、S四边形OABC.
解答: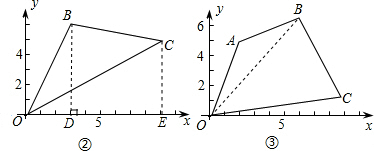 解:(1)过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.
解:(1)过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.
S△OBC=S梯形BCED+S△OBD-S△OCE
=
(y1+y2)(x2-x1)+
x1y1-
x2y2
=
(x2y1-x1y2)
=
x2y1-
x1y2.
∴△BOC的面积为
x2y1-
x1y2.
(2)连接OB.
则有S四边形OABC=S△OAB+S△OBC
=
×7×5-
×2×7+
×9×7-
×7×1
=38.5.
∴四边形OABC的面积为38.5.
 解:(1)过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.
解:(1)过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.S△OBC=S梯形BCED+S△OBD-S△OCE
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
∴△BOC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
(2)连接OB.
则有S四边形OABC=S△OAB+S△OBC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=38.5.
∴四边形OABC的面积为38.5.
点评:本题考查了三角形的面积、坐标与图形的性质.需要掌握点的坐标的意义以及与图形相结合的解题方法.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
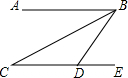 (2007•海淀区二模)如图,BC平分∠ABD,AB∥CD,点E在CD的延长线上.若∠C=28°,则∠BDE的度数为( )
(2007•海淀区二模)如图,BC平分∠ABD,AB∥CD,点E在CD的延长线上.若∠C=28°,则∠BDE的度数为( ) (2007•海淀区二模)北京奥运会金牌创造性地将白玉圆环嵌在其中(如图),这一设计不仅是对获胜者的礼赞,也形象地诠释了中华民族自古以来以“玉”比“德”的价值观.若白玉圆环面积与整个金牌面积的比值为k,则下列各数与k最接近的是( )
(2007•海淀区二模)北京奥运会金牌创造性地将白玉圆环嵌在其中(如图),这一设计不仅是对获胜者的礼赞,也形象地诠释了中华民族自古以来以“玉”比“德”的价值观.若白玉圆环面积与整个金牌面积的比值为k,则下列各数与k最接近的是( ) (2007•海淀区二模)用“¤”定义一种运算:对于任意实数m、n和抛物线y=ax2,当y=ax2¤(m,n)后都可得到y=a(x-m)2+n.例如:当y=3x2¤(2,4)后得到y=3(x-2)2+4.当函数y=x2¤(1,n)后得到了新函数的图象(如图所示),则n=
(2007•海淀区二模)用“¤”定义一种运算:对于任意实数m、n和抛物线y=ax2,当y=ax2¤(m,n)后都可得到y=a(x-m)2+n.例如:当y=3x2¤(2,4)后得到y=3(x-2)2+4.当函数y=x2¤(1,n)后得到了新函数的图象(如图所示),则n=