摘要:对两位同学计算重力加速度的方法作出评价,如果合理请说出理由.如果存在问题请指出,并给出你认为合理的计算方法.
网址:http://m.1010jiajiao.com/timu_id_3738[举报]
在用单摆测重力加速度的实验中:
(1)应注意,实验时必须控制摆角在______内,并且要让单摆在______内摆动.
(2)测量单摆周期时,等单摆自由振动几次之后,从摆球经过______位置时开始计时,因为这时摆球的速度______,可以减少误差.
(3)某同学测出不同摆长时对应的周期T,作出L-T2图线,如图所示,再利用图线上任意两点A、B的坐标(x1,y1)、(x2,y2),可求得g=______.
(4)若该同学测摆长时漏加了小球半径,而其他测量、计算均无误,也不考虑实验误差,则以上方法得的g值和真实值相比是______的(“偏大”“偏小”或“不变”).
查看习题详情和答案>>
(1)应注意,实验时必须控制摆角在______内,并且要让单摆在______内摆动.
(2)测量单摆周期时,等单摆自由振动几次之后,从摆球经过______位置时开始计时,因为这时摆球的速度______,可以减少误差.
(3)某同学测出不同摆长时对应的周期T,作出L-T2图线,如图所示,再利用图线上任意两点A、B的坐标(x1,y1)、(x2,y2),可求得g=______.
(4)若该同学测摆长时漏加了小球半径,而其他测量、计算均无误,也不考虑实验误差,则以上方法得的g值和真实值相比是______的(“偏大”“偏小”或“不变”).

在用单摆测重力加速度的实验中:
(1)应注意,实验时必须控制摆角在 内,并且要让单摆在 内摆动.
(2)测量单摆周期时,等单摆自由振动几次之后,从摆球经过 位置时开始计时,因为这时摆球的速度 ,可以减少误差.
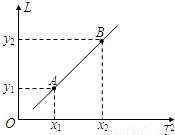
(3)某同学测出不同摆长时对应的周期T,作出L-T2图线,如图所示,再利用图线上任意两点A、B的坐标(x1,y1)、(x2,y2),可求得g= .
(4)若该同学测摆长时漏加了小球半径,而其他测量、计算均无误,也不考虑实验误差,则以上方法得的g值和真实值相比是 的(“偏大”“偏小”或“不变”).
 查看习题详情和答案>>
查看习题详情和答案>>
(1)应注意,实验时必须控制摆角在 内,并且要让单摆在 内摆动.
(2)测量单摆周期时,等单摆自由振动几次之后,从摆球经过 位置时开始计时,因为这时摆球的速度 ,可以减少误差.
(3)某同学测出不同摆长时对应的周期T,作出L-T2图线,如图所示,再利用图线上任意两点A、B的坐标(x1,y1)、(x2,y2),可求得g= .
(4)若该同学测摆长时漏加了小球半径,而其他测量、计算均无误,也不考虑实验误差,则以上方法得的g值和真实值相比是 的(“偏大”“偏小”或“不变”).
 查看习题详情和答案>>
查看习题详情和答案>>
在用单摆测重力加速度的实验中:
(1)应注意,实验时必须控制摆角在 内,并且要让单摆在 内摆动.
(2)测量单摆周期时,等单摆自由振动几次之后,从摆球经过 位置时开始计时,因为这时摆球的速度 ,可以减少误差.
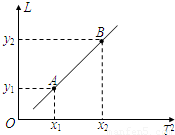
(3)某同学测出不同摆长时对应的周期T,作出L-T2图线,如图所示,再利用图线上任意两点A、B的坐标(x1,y1)、(x2,y2),可求得g= .
(4)若该同学测摆长时漏加了小球半径,而其他测量、计算均无误,也不考虑实验误差,则以上方法得的g值和真实值相比是 的(“偏大”“偏小”或“不变”).
 查看习题详情和答案>>
查看习题详情和答案>>
(1)应注意,实验时必须控制摆角在 内,并且要让单摆在 内摆动.
(2)测量单摆周期时,等单摆自由振动几次之后,从摆球经过 位置时开始计时,因为这时摆球的速度 ,可以减少误差.
(3)某同学测出不同摆长时对应的周期T,作出L-T2图线,如图所示,再利用图线上任意两点A、B的坐标(x1,y1)、(x2,y2),可求得g= .
(4)若该同学测摆长时漏加了小球半径,而其他测量、计算均无误,也不考虑实验误差,则以上方法得的g值和真实值相比是 的(“偏大”“偏小”或“不变”).
 查看习题详情和答案>>
查看习题详情和答案>>
在用单摆测重力加速度的实验中:
(1)应注意,实验时必须控制摆角在 内,并且要让单摆在 内摆动.
(2)测量单摆周期时,等单摆自由振动几次之后,从摆球经过 位置时开始计时,因为这时摆球的速度 ,可以减少误差.
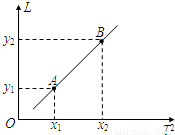
(3)某同学测出不同摆长时对应的周期T,作出L-T2图线,如图所示,再利用图线上任意两点A、B的坐标(x1,y1)、(x2,y2),可求得g= .
(4)若该同学测摆长时漏加了小球半径,而其他测量、计算均无误,也不考虑实验误差,则以上方法得的g值和真实值相比是 的(“偏大”“偏小”或“不变”).
 查看习题详情和答案>>
查看习题详情和答案>>
(1)应注意,实验时必须控制摆角在 内,并且要让单摆在 内摆动.
(2)测量单摆周期时,等单摆自由振动几次之后,从摆球经过 位置时开始计时,因为这时摆球的速度 ,可以减少误差.
(3)某同学测出不同摆长时对应的周期T,作出L-T2图线,如图所示,再利用图线上任意两点A、B的坐标(x1,y1)、(x2,y2),可求得g= .
(4)若该同学测摆长时漏加了小球半径,而其他测量、计算均无误,也不考虑实验误差,则以上方法得的g值和真实值相比是 的(“偏大”“偏小”或“不变”).
 查看习题详情和答案>>
查看习题详情和答案>>
在“用单摆测定重力加速度”的实验中:
(1)摆动时偏角满足的条件是
.
(2)用最小刻度为1mm的刻度尺测摆线长度,测量情况如图(2)所示.O为悬挂点,从图中可知单摆的摆线长度L0=
(3)用游标卡尺测小球直径如图(1)所示,则小球直径d=
(4)若用T表示周期,那么重力加速度的表达式为g=
.(用T,L0,d表示)
(5)考虑到单摆振动时空气浮力的影响后,学生甲说:“因为空气浮力与摆球重力方向相反,它对球的作用相当于重力加速度变小,因此振动周期变大.”学生乙说:“浮力对摆球的影响好像用一个轻一些的摆球做实验,因此振动周期不变”,这两个学生中
A.甲的说法正确 B.乙的说法正确 C.两学生的说法都是错误的

(6)在利用单摆测定重力加速度的实验中,若某同学测出了多组摆长和运动周期,根据实验数据,作出的T2-l关系图象如
图(3)所示.
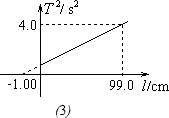
(a)该同学实验中出现的错误可能是
(b)虽然实验中出现了错误,但根据图象中的数据,仍可准确算出重力加速度,其值为
查看习题详情和答案>>
(1)摆动时偏角满足的条件是
小于5°
小于5°
,为了减小测量周期的误差,摆球应是经过最低
低
(填“高”或“低’)的点的位置,开始计时并计数l次,测出经过该位置N次的时间为t,则周期为| t |
| N-1 |
| t |
| N-1 |
(2)用最小刻度为1mm的刻度尺测摆线长度,测量情况如图(2)所示.O为悬挂点,从图中可知单摆的摆线长度L0=
0.9910
0.9910
m.(3)用游标卡尺测小球直径如图(1)所示,则小球直径d=
8.55
8.55
mm;(4)若用T表示周期,那么重力加速度的表达式为g=
4π2(l0+
| ||
| T2 |
4π2(l0+
| ||
| T2 |
(5)考虑到单摆振动时空气浮力的影响后,学生甲说:“因为空气浮力与摆球重力方向相反,它对球的作用相当于重力加速度变小,因此振动周期变大.”学生乙说:“浮力对摆球的影响好像用一个轻一些的摆球做实验,因此振动周期不变”,这两个学生中
A
A
.A.甲的说法正确 B.乙的说法正确 C.两学生的说法都是错误的

(6)在利用单摆测定重力加速度的实验中,若某同学测出了多组摆长和运动周期,根据实验数据,作出的T2-l关系图象如
图(3)所示.

(a)该同学实验中出现的错误可能是
将摆线的长度当作摆长
将摆线的长度当作摆长
(b)虽然实验中出现了错误,但根据图象中的数据,仍可准确算出重力加速度,其值为
9.86
9.86
m/s2.