题目内容
在用单摆测重力加速度的实验中:(1)应注意,实验时必须控制摆角在 内,并且要让单摆在 内摆动.
(2)测量单摆周期时,等单摆自由振动几次之后,从摆球经过 位置时开始计时,因为这时摆球的速度 ,可以减少误差.
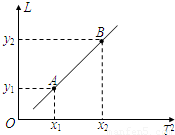
(3)某同学测出不同摆长时对应的周期T,作出L-T2图线,如图所示,再利用图线上任意两点A、B的坐标(x1,y1)、(x2,y2),可求得g= .
(4)若该同学测摆长时漏加了小球半径,而其他测量、计算均无误,也不考虑实验误差,则以上方法得的g值和真实值相比是 的(“偏大”“偏小”或“不变”).
【答案】分析:(1)单摆模型是一种理想化的模型,只有在摆动角度小于5°(或10°)的范围内,其运动才近似为简谐运动,同时要注意不能做圆锥摆运动,否则误差较大;
(2)测量周期要尽量减小偶然误差,应该从摆球经过最低位置时开始计时,因为这时摆球的速度最大可以减少误差;
(3)用图想法可以减小实验误差,而且图象直观形象,便于数据处理;
(4)漏加了小球半径后,直线的斜率不变,故不影响最后结果.
解答:解:(1)单摆模型是一种理想化的模型,只有在摆动角度小于5°(或10°)的范围内,其运动才近似为简谐运动,同时要注意不能做圆锥摆运动
故答案为:5°或10°,同一竖直平面.
(2)测量周期要尽量减小偶然误差,应该从摆球经过最低位置时开始计时,因为这时摆球的速度最大可以减少误差
故答案为:最低,最大.
(3)由周期公式T=2π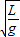 ,可得
,可得
L=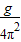 T2
T2
代入数据可得
g=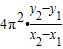
故答案为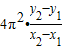 .
.
(4)通过第(3)问的结论可以知道,漏加了小球半径后(y2-y1)不变,故不影响最后结果
故答案为:不变.
点评:用单摆测重力加速度是一种简单且便于操作的方法,要注意尽量减小实验误差,摆动角度要小,数据处理尽量用图象法.
(2)测量周期要尽量减小偶然误差,应该从摆球经过最低位置时开始计时,因为这时摆球的速度最大可以减少误差;
(3)用图想法可以减小实验误差,而且图象直观形象,便于数据处理;
(4)漏加了小球半径后,直线的斜率不变,故不影响最后结果.
解答:解:(1)单摆模型是一种理想化的模型,只有在摆动角度小于5°(或10°)的范围内,其运动才近似为简谐运动,同时要注意不能做圆锥摆运动
故答案为:5°或10°,同一竖直平面.
(2)测量周期要尽量减小偶然误差,应该从摆球经过最低位置时开始计时,因为这时摆球的速度最大可以减少误差
故答案为:最低,最大.
(3)由周期公式T=2π
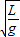 ,可得
,可得L=
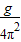 T2
T2代入数据可得
g=
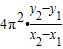
故答案为
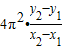 .
.(4)通过第(3)问的结论可以知道,漏加了小球半径后(y2-y1)不变,故不影响最后结果
故答案为:不变.
点评:用单摆测重力加速度是一种简单且便于操作的方法,要注意尽量减小实验误差,摆动角度要小,数据处理尽量用图象法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在“用单摆测重力加速度”的实验中,
在“用单摆测重力加速度”的实验中,