摘要:(Ⅱ)当k为偶数时.数列{}满足.证明:数列{}中不存在成等差数列的三项,
网址:http://m.1010jiajiao.com/timu_id_371103[举报]












设函数![]() 表示f(x)导函数。
表示f(x)导函数。
(I)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{![]() }满足
}满足![]() .证明:数列{
.证明:数列{![]() }中
}中
不存在成等差数列的三项;
(Ⅲ)当后为奇数时,证明:对任意正整数,n都有![]() 成立.
成立.
设函数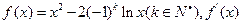 表示f(x)导函数。
表示f(x)导函数。
(I)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{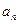 }满足
}满足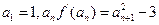 .证明:数列{
.证明:数列{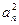 }中
}中
不存在成等差数列的三项;
(Ⅲ)当后为奇数时,证明:对任意正整数,n都有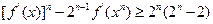 成立.
成立.
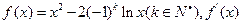 表示f(x)导函数。
表示f(x)导函数。(I)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{
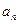 }满足
}满足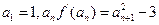 .证明:数列{
.证明:数列{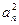 }中
}中不存在成等差数列的三项;
(Ⅲ)当后为奇数时,证明:对任意正整数,n都有
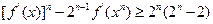 成立.
成立.(09年潍坊一模文)(14分)
设函数![]() 表示f(x)导函数。
表示f(x)导函数。
(I)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{![]() }满足
}满足![]() .证明:数列{
.证明:数列{![]() }中
}中
不存在成等差数列的三项;
(Ⅲ)当后为奇数时,证明:对任意正整数,n都有![]() 成立.
成立.