摘要:解得.
网址:http://m.1010jiajiao.com/timu_id_370372[举报]
先阅读下面的文字:“求
的值时,采用了如下的方式:令
=x,则有x=
,两边平方,得1+x=x2,解得x=
(负值已舍去)”.可用类比的方法,求2+
的值为
查看习题详情和答案>>
1+
|
1+
|
| 1+x |
1+
| ||
| 2 |
| 1 | ||
2+
|
1+
| 2 |
1+
.| 2 |
已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当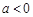 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
查看习题详情和答案>>
阅读材料:某同学求解sin18°的值其过程为:设α=18°,则5α=90°,从而3α=90°-2α,于是cos3α=cos(90°-2α),即cos3α=sin2α,展开得4cos3α-3cosα=2sinαcosα,∴cosα=cos18°≠0,∴4cos2α-3=2sinα,化简,得4sin2α+2sinα-1=0,解得sinα=
,∵sinα=sin18°∈(0,1),∴sinα=
(sinα=
<0舍去),即sin18°=
.试完成以下填空:设函数f(x)=ax3+1对任意x∈[-1,1]都有f(x)≥0成立,则实数a的值为
查看习题详情和答案>>
-1±
| ||
| 4 |
-1+
| ||
| 4 |
-1-
| ||
| 4 |
-1+
| ||
| 4 |
4
4
. 夹角为
夹角为 ,且
,且 ;则
;则
 ,所以
,所以 ,即
,即 ,所以
,所以 ,整理得
,整理得 ,解得
,解得 或
或 (舍去).
(舍去). 的值时,采用了如下的方式:令
的值时,采用了如下的方式:令 ,则有
,则有 ,两边平方,得1+x=x2,解得
,两边平方,得1+x=x2,解得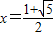 (负值已舍去)”.可用类比的方法,求
(负值已舍去)”.可用类比的方法,求 的值为 .
的值为 .