网址:http://m.1010jiajiao.com/timu_id_36289[举报]
一、选择题:(每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
A
D
D
A
B
C
C
D
二、填空题:(每小题5分,共30分)
11.  ; 12.
; 12.  ; 13.
; 13.  ; 14. 2或
; 14. 2或 ; 15.
; 15.  ; 16. 9.
; 16. 9.
三、解答题:(5大题,共70分)
17.(1)由 ,得
,得 ------------3分
------------3分
 为锐角,
为锐角, , -------5分
, -------5分
 --------------------------6分
--------------------------6分
(2)
 ---8分
---8分
又 ,
, ,得
,得 ,
--------------------------10分
,
--------------------------10分
 --------------------------12分
--------------------------12分
(若通过 得出
得出 ,求出
,求出 ,
,
未舍去 ,
, 得两解,扣2分.)
得两解,扣2分.)
18.(1)设点 ,由
,由 得
得 ,
, ,
,
由 ,得
,得 , ------------------------4分
, ------------------------4分
即 .
---------------------6分
.
---------------------6分
(2)由(1)知 为抛物线
为抛物线 :
: 的焦点,
的焦点, 为过焦点
为过焦点 的直线与
的直线与 的两个交点.
的两个交点.
①当直线 斜率不存在时,得
斜率不存在时,得 ,
, ,
, . ----8分
. ----8分
②当直线斜率存在且不为0时,设 ,代入
,代入 得
得
 .设
.设 ,
,
则 ,得
,得 , ----12分
, ----12分
(或 )
)
 ,此时
,此时 ,由
,由 得
得
 。
---------------14分
。
---------------14分
19.解法一:
(1)在 中,
中, ,
, ,
,
∴
 ,取
,取 中点
中点 ,
,
 ,
,  ,
,
在 中,
中, ,
, ,又
,又 均为锐角,∴
均为锐角,∴ , ---------------2分
, ---------------2分
 ,又
,又 外,
外,  . ---------------4分
. ---------------4分
(2)∵平面
 平面
平面 ,∴
,∴ ,过
,过 作
作 于
于 ,连结
,连结 ,则
,则 ,
,
 为二面角
为二面角 的平面角, ------------------------6分
的平面角, ------------------------6分
易知 =
= ,∴
,∴ ,
,
 二面角
二面角 的大小为
的大小为 . ------------------------9分
. ------------------------9分
(其它等价答案给同样的得分)
(3) ,
, 点到平面
点到平面 的距离,就是
的距离,就是 到平面
到平面 的距离,-------------------------------11分
的距离,-------------------------------11分
过 作
作 于
于 ,则
,则 ,
, 的长度即为所求, 由上
的长度即为所求, 由上 (或用等体积
(或用等体积 求)----------------------------------14分
求)----------------------------------14分
解法二:
如图,建立图示空间直角坐标系.
则 ,
, ,
, ,
, ,
, .
.
(1)
(2)利用 ,其中
,其中 分别为两个半平面的法向量,
分别为两个半平面的法向量,
或利用 求解.
求解.
(3)利用 ,其中
,其中 为平面
为平面 的法向量。
的法向量。
20.(1) ,∴
,∴ ①
①
又 ,∴
,∴ ,即
,即 ②
②
由①②得 ,
, .又
.又 时,①、②不成立,故
时,①、②不成立,故 .------2分
.------2分
∴ ,设x1、x2是函数
,设x1、x2是函数 的两个极值点,则x1、x2是方程
的两个极值点,则x1、x2是方程 =0的两个根,
=0的两个根, ,
,
∴x1+x2= ,又∵ A、O、B三点共线,
,又∵ A、O、B三点共线,
 =
= ,
,
∴ =0,又∵x1≠x2,∴b= x1+x2=
=0,又∵x1≠x2,∴b= x1+x2= ,∴b=0. ----------------6分
,∴b=0. ----------------6分
(2) 时,
时, ,
-----------------------7分
,
-----------------------7分
由 得
得 ,可知
,可知 在
在 上单调递增,在
上单调递增,在
上单调递减,
 . ---------------------9分
. ---------------------9分
①由 得
得
 的值为1或2.(∵
的值为1或2.(∵ 为正整数) -----------------11分
为正整数) -----------------11分
② 时,记
时,记 在
在 上切线斜率为2的切点的横坐标为
上切线斜率为2的切点的横坐标为 ,
,
则由 得
得 ,依题意得
,依题意得 ,
,
 得
得 与
与 矛盾.
矛盾.
(或构造函数 在
在 上恒正)
上恒正)
综上,所求 的值为1或2.
-----------------------14分
的值为1或2.
-----------------------14分
21.(1)∵ 为正数,
为正数, ①,
①, =1,∴
=1,∴ >0(n∈N*),……… 1分
>0(n∈N*),……… 1分
又 ②,①―②两式相减得
②,①―②两式相减得 ,
,
∴ 与
与 同号,
---------------------4分
同号,
---------------------4分
∴ 对n∈N*恒成立的充要条件是
对n∈N*恒成立的充要条件是 >0.
---------------------7分
>0.
---------------------7分
由 =
= >0,得
>0,得 >7 .
---------------------8分
>7 .
---------------------8分
(2)证法1:假设存在 ,使得对任意正整数
,使得对任意正整数 都有
都有 .
.
则 ,则
,则 >17 .
--------------------9分
>17 .
--------------------9分
另一方面, =
= =
=
 ,---------11分
,---------11分
∴
 ,
,
 ,……,
,……,
 ,
,
∴
 ,∴
,∴
 =
= , ①
, ①
--------------------------------14分
当m>16时,由①知, ,不可能使
,不可能使 对任意正整数n恒成立,
对任意正整数n恒成立,
--------------------------------15分
∴m≤16,这与 >17矛盾,故不存在m,使得对任意正整数n都有
>17矛盾,故不存在m,使得对任意正整数n都有 .
.
--------------------------------16分
(2)证法2:假设存在m,使得对任意正整数n都有 .
.
则 ,则
,则 >17 .
--------------------9分
>17 .
--------------------9分
另一方面, ,
------------------11分
,
------------------11分
∴ ,
, ,……,
,……, ,
,
∴ ,
, ①
-----------------14分
①
-----------------14分
当m>16时,由①知, ,不可能使
,不可能使 对任意正整数恒成立,
对任意正整数恒成立,
--------------------------15分
∴m≤16,这与 >17矛盾,故不存在m,使得对任意正整数n都有
>17矛盾,故不存在m,使得对任意正整数n都有 。
-----------------------------16分
。
-----------------------------16分
C.选修4-4:坐标系与参数方程
在极坐标系下,已知圆O: 和直线
和直线 ,
,
(1)求圆O和直线 的直角坐标方程;(2)当
的直角坐标方程;(2)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
D.选修4-5:不等式证明选讲
对于任意实数
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
在极坐标系下,已知圆O:
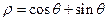 和直线
和直线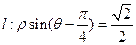 ,
,(1)求圆O和直线
 的直角坐标方程;(2)当
的直角坐标方程;(2)当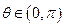 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.D.选修4-5:不等式证明选讲
对于任意实数
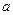
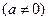 和
和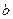 ,不等式
,不等式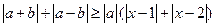 恒成立,试求实数
恒成立,试求实数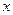 的取值范围.
的取值范围.









 作圆
作圆 的弦,其中弦长为整数的共有 ( )
的弦,其中弦长为整数的共有 ( )