网址:http://m.1010jiajiao.com/timu_id_354[举报]
1、18,9.
2、-1。 3、3。27534×1011 4、,.files/image021.gif) ,等 5、3,(-2,-3)
,等 5、3,(-2,-3)
6、AB方向,1 7、75°或105° 8、黄色 9、1200元 10、40%
11、C 12、B 13、B 14、B 15、B 16、C 17、C 18、A 19、C 20、C
21、4+2 22、长为15米,宽为10米 23、240000千克
24、解:设旗杆在高楼上的影子为DC,连结AC并延长,交BD的延长线于E,
根据题意,=1.5:1,DE=1.5CD=3,
因为BE=BD+DE,BD=21,所以BE=24
又因为AB:BE=1:1.5,
所以AB=24/1.5=16,即旗杆的高度为16米。
25、方案一、生产A种产品30件,生产B种产品20件。
方案二、生产A种产品31件,生产B种产品19件。
方案三、生产A种产品32件,生产B种产品18件。
26、(1)AE×BE 12.02 15 14.95
CE×DE 12.01 15.02 15
(2) AE×BE=CE×DE,用相似证明相交弦定理。
(3)由相交弦定理,(R+5)(R-5)=24,得R=7
27、解:(1)设经过t小时后汽车受到了台风的影响,
此时汽车行驶到了点B,台风中心移到点C,
则OB=40t,AC=20t,
作CP⊥OB于点P,CQ⊥OA于点Q,
则AQ=20t,CQ=20t,
所以BP=OB-OP=OB-CQ=20t,CP=OQ=OA-AQ=160-20t,
由BP2+CP2=BC2,得(20t)2+(160-20t)2=1202,
化简得t2-8t+14=0,解得t1=4-,t2=4+,
所以,经过4-小时后,汽车受到台风影响。
(2)当t1≤t≤t2时,(20t)2+(160-20t)2≤1202,
所以在t1到t2这段时间内,汽车一直受到台风影响,
因为ㄏt1-t2ㄏ=2,
所以汽车受台风影响的时间为2小时。毛
.files/image023.jpg) |
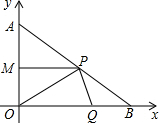 分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)
分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)(1)过点P做PM⊥OA于M,求证:AM:AO=PM:BO=AP:AB,并求出P点的坐标(用t表示);
(2)求△OPQ面积S(cm2),与运动时间t(秒)之间的函数关系式,当t为何值时,S有最大值?最大是多少?
(3)当t为何值时,△OPQ为直角三角形?
(4)证明无论t为何值时,△OPQ都不可能为正三角形.若点P运动速度不变改变Q的运动速度,使△OPQ为正三角形,求Q点运动的速度和此时t的值. 查看习题详情和答案>>
 匀速运动,速度均为1cm/秒,设P、Q运动时间为t(0≤t≤4)
匀速运动,速度均为1cm/秒,设P、Q运动时间为t(0≤t≤4)(1)AB的长为
(2)过点P做PM⊥OA于M,则P点的坐标为
(3)求△OPQ面积S(cm2)与运动时间t(秒)之间的函数关系式,当t为何值时,S有最大值?最大是多少?
(4)探究△OPQ能否为直角三角形,若能,请直接写出t的值;若不能,请说明理由. 查看习题详情和答案>>
如图,在Rt△AOB中,∠AOB=90°,OA=3cm,OB=4cm,以点O为坐标原点建立坐标系,设P、Q 分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)
分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)
(1)过点P做PM⊥OA于M,求证:AM:AO=PM:BO=AP:AB,并求出P点的坐标(用t表示);
(2)求△OPQ面积S(cm2),与运动时间t(秒)之间的函数关系式,当t为何值时,S有最大值?最大是多少?
(3)当t为何值时,△OPQ为直角三角形?
(4)证明无论t为何值时,△OPQ都不可能为正三角形.若点P运动速度不变改变Q的运动速度,使△OPQ为正三角形,求Q点运动的速度和此时t的值.
查看习题详情和答案>>
如图,在Rt△AOB中,∠AOB=90°,OA=3cm,OB=4cm,以点O为坐标原点建立坐标系,设P、Q分别为AB、OB边上的动点它们同时分别从点A、O向B点 匀速运动,速度均为1cm/秒,设P、Q运动时间为t(0≤t≤4)
匀速运动,速度均为1cm/秒,设P、Q运动时间为t(0≤t≤4)
(1)AB的长为______cm.
(2)过点P做PM⊥OA于M,则P点的坐标为______(用含t的代数式表示).
(3)求△OPQ面积S(cm2)与运动时间t(秒)之间的函数关系式,当t为何值时,S有最大值?最大是多少?
(4)探究△OPQ能否为直角三角形,若能,请直接写出t的值;若不能,请说明理由.
查看习题详情和答案>>
(1)求运动t秒时,P,Q两点的坐标.(用含t的式子表示).
(2)若△OPQ的面积为Scm2,运动的时间为t秒,求S与t之间的函数关系式.当t为何值时,S有最大值?最大面积是多少?
(3)当t为何值时,直线PQ将△AOB的面积分成1:3两部分?
(4)按此速度运动下去,△OPQ能否成为正三角形?若能,求出时间t;若不能,请说明理由.能否通过改变Q点的速度,使△OPQ成为正三角形?若能,请求出改变后Q的速度和此时t的值.
 查看习题详情和答案>>
查看习题详情和答案>>