网址:http://m.1010jiajiao.com/timu_id_345825[举报]
一、填空题
1、/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image249.gif) 2、40 3、②
④) 4、-1 5、
2、40 3、②
④) 4、-1 5、/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image251.gif) 6、3
6、3
7、/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image253.gif) 8、
8、/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image255.gif) 9、1 10、
9、1 10、/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image257.gif) 11、
11、/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image259.gif) 12、46 13、
12、46 13、/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image261.gif)
14、(3)(4)
二、解答题
15、解:(1)∵a⊥b,∴a?b=0.而a=(3sinα,cosα),b=(2sinα, 5sinα-4cosα),
故a?b=6sin2α+5sinαcosα-4cos2α=0.……………………………………2分
由于cosα≠0,∴6tan2α+5tanα-4 =0.解之,得tanα=-/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image263.gif) ,或tanα=
,或tanα=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image265.gif) .……………………………………………6分
.……………………………………………6分
∵α∈(/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image141.gif) ),tanα<0,故tanα=
),tanα<0,故tanα=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image265.gif) (舍去).∴tanα=-
(舍去).∴tanα=-/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image263.gif) .…………7分
.…………7分
(2)∵α∈(/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image141.gif) ),∴
),∴/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image267.gif) .
.
由tanα=-/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image263.gif) ,求得
,求得/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image269.gif) ,
,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image271.gif) =2(舍去).
=2(舍去).
∴/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image273.gif) ,…………………………………………………………12分
,…………………………………………………………12分
cos(/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image275.gif) )=
)=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image277.gif)
=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image279.gif) =
=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image281.gif) . ………………………14分
. ………………………14分
16、证明:(1)连结/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image283.gif) ,在
,在/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image285.gif) 中,
中,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image146.gif) 、
、/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image148.gif) 分别为
分别为/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image289.gif) ,
,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image151.gif) 的中点,则
的中点,则
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image291.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image293.gif)
(2)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image295.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image297.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image299.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image301.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image303.gif)
(3)/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image305.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image307.gif) 且
且 /江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image309.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image311.gif) ,
,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image313.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image315.gif)
∴/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image317.gif) 即
即/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image319.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image321.gif) =
=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image323.gif)
=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image325.gif)
17、解:由已知圆的方程为/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image327.gif) ,
,
按/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image329.gif) 平移得到
平移得到/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image331.gif) .
.
∵/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image333.gif) ∴
∴/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image335.gif) .
.
即/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image337.gif) .
.
又/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image339.gif) ,且
,且/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image329.gif) ,∴
,∴/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image342.gif) .∴
.∴/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image344.gif) .
.
设/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image346.gif) ,
, /江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image348.gif) 的中点为D.
的中点为D.
由/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image350.gif) ,则
,则/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image352.gif) ,又
,又/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image354.gif) .
.
∴/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image356.gif) 到
到/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image358.gif) 的距离等于
的距离等于/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image360.gif) .
.
即/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image362.gif) , ∴
, ∴/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image364.gif) .
.
∴直线/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image167.gif) 的方程为:
的方程为:/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image367.gif) 或
或/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image369.gif) .
.
18、(1)在△ADE中,y2=x2+AE2-2x?AE?cos60°/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image297.gif) y2=x2+AE2-x?AE,①
y2=x2+AE2-x?AE,①
又S△ADE=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image372.gif) S△ABC=
S△ABC=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image374.gif) a2=
a2=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image372.gif) x?AE?sin60°
x?AE?sin60°/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image297.gif) x?AE=2.②
x?AE=2.②
②代入①得y2=x2+/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image377.gif) -2(y>0), ∴y=
-2(y>0), ∴y=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image379.gif) (1≤x≤2)。。。.6分
(1≤x≤2)。。。.6分
(2)如果DE是水管y=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image379.gif) ≥
≥/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image382.gif) ,
,
当且仅当x2=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image384.gif) ,即x=
,即x=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image386.gif) 时“=”成立,故DE∥BC,且DE=
时“=”成立,故DE∥BC,且DE=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image386.gif) .
.
如果DE是参观线路,记f(x)=x2+/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image384.gif) ,可知
,可知
函数在[1,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image386.gif) ]上递减,在[
]上递减,在[/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image386.gif) ,2]上递增,
,2]上递增,
故f(x) max=f(1)=f(2)=5. ∴y max=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image388.gif) .
.
即DE为AB中线或AC中线时,DE最长.。。。。。。。。。。。8分
19、解:(1)由/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image390.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image392.gif) 是首项为
是首项为/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image394.gif) ,公比为
,公比为/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image396.gif) 的等比数列
的等比数列
当/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image398.gif) 时,
时,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image400.gif) ,
,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image402.gif)
所以 /江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image404.gif)
(2)由/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image406.gif) 得:
得:/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image408.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image410.gif) (作差证明)
(作差证明)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image412.gif)
综上所述当/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image414.gif) 时,不等式
时,不等式/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image204.gif) 对任意
对任意/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image206.gif) 都成立.
都成立.
20.解.(1)/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image417.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image419.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image421.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image423.gif) 当
当/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image425.gif) 时,
时,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image427.gif) ,此时
,此时/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image429.gif) 为单调递减
为单调递减
当/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image431.gif) 时,
时,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image433.gif) ,此时
,此时/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image429.gif) 为单调递增
为单调递增
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image423.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image429.gif) 的极小值为
的极小值为/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image437.gif)
(2)/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image417.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image429.gif) 的极小值,即
的极小值,即/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image429.gif) 在
在/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image441.gif) 的最小值为1
的最小值为1
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image423.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image443.gif) 令
令/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image445.gif)
又/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image417.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image447.gif) 当
当/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image449.gif) 时
时/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image451.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image453.gif) 在
在/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image441.gif) 上单调递减
上单调递减
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image423.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image456.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image423.gif) 当
当/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image458.gif) 时,
时,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image460.gif)
(3)假设存在实数/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image220.gif) ,使
,使/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image463.gif) 有最小值3,
有最小值3,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image458.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image466.gif)
①当/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image468.gif) 时,由于
时,由于/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image458.gif) ,则
,则/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image470.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image423.gif) 函数
函数/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image463.gif) 是
是/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image441.gif) 上的增函数
上的增函数
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image423.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image473.gif)
解得/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image475.gif) (舍去)
(舍去)
②当/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image477.gif) 时,则当
时,则当/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image479.gif) 时,
时,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image481.gif)
此时/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image463.gif) 是减函数
是减函数
当/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image483.gif) 时,
时,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image485.gif) ,此时
,此时/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image463.gif) 是增函数
是增函数
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image423.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image487.gif)
解得/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image489.gif)
理科加试题
1、(1)“油罐被引爆”的事件为事件A,其对立事件为/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image491.gif) ,则P(
,则P(/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image491.gif) )=C
)=C/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image494.gif)
∴P(A)=1-/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image496.gif) 答:油罐被引爆的概率为
答:油罐被引爆的概率为/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image498.gif)
(2)射击次数ξ的可能取值为2,3,4,5,
P(ξ=2)=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image500.gif) , P(ξ=3)=C
, P(ξ=3)=C/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image502.gif) ,
,
P(ξ=4)=C/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image504.gif) , P(ξ=5)=C
, P(ξ=5)=C/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image506.gif)
ξ
2
3
4
5
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image508.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image510.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image512.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image514.gif)
故ξ的分布列为:
Eξ=2×/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image508.gif) +3×
+3×/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image510.gif) +4×
+4×/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image512.gif) +5×
+5×/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image514.gif) =
=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image516.gif)
2、解:(1)由图形可知二次函数的图象过点(0,0),(8,0),并且f(x)的最大值为16
则/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image518.gif) ,
,
∴函数f(x)的解析式为/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image520.gif)
(2)由/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image522.gif) 得
得/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image524.gif)
∵0≤t≤2,∴直线l1与f(x)的图象的交点坐标为(/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image526.gif)
由定积分的几何意义知:
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image528.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image530.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image532.gif)
3、解:在矩阵N=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image236.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image241.gif) 的作用下,一个图形变换为其绕原点逆时针旋转
的作用下,一个图形变换为其绕原点逆时针旋转/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image534.gif) 得到的图形,在矩阵M=
得到的图形,在矩阵M=/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image236.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image238.gif) 的作用下,一个图形变换为与之关于直线
的作用下,一个图形变换为与之关于直线/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image536.gif) 对称的图形。因此
对称的图形。因此
△ABC在矩阵MN作用下变换所得到的图形与△ABC全等,从而其面积等于△ABC的面积,即为1
4、解:以极点为原点,极轴为/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image114.gif) 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(1)/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image539.gif) ,
,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image541.gif) ,由
,由/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image543.gif) 得
得/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image545.gif) .
.
所以/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image547.gif) .
.
即/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image549.gif) 为
为/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image243.gif) 的直角坐标方程.
的直角坐标方程.
同理/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image552.gif) 为
为/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image245.gif) 的直角坐标方程.
的直角坐标方程.
(2)由/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image555.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image557.gif) 解得
解得/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image559.gif)
/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image561.gif) .
.
即/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image243.gif) ,
,/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image245.gif) 交于点
交于点/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image563.gif) 和
和/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image565.gif) .过交点的直线的直角坐标方程为
.过交点的直线的直角坐标方程为/江苏省泰州市2008-2009学年第一学期期末联考高三数学模拟试题.files/image567.gif) .
.
(12分) 已知二次函数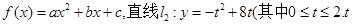
为常数);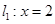 .若直线
.若直线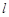 1、
1、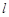 2与函数
2与函数 的图象以及
的图象以及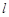 2,y轴与函数
2,y轴与函数 的图象
的图象
所围成的封闭图形如阴影所示.
(1)求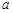 、b、c的值;
、b、c的值;
(2)求阴影面积S关于t的函数S(t)的解析式;
(3)若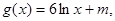 问是否存在实数m,使得
问是否存在实数m,使得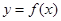 的图象与
的图象与 的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
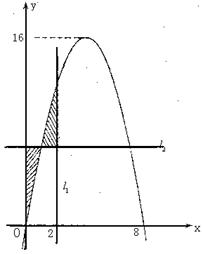
查看习题详情和答案>>
(12分)已知二次函数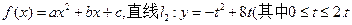
为常数) ;
;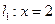 .若直线
.若直线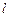 1、
1、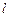 2与函数
2与函数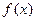 的图象以及
的图象以及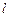 2,y轴与函数
2,y轴与函数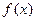 的图象
的图象
所围成的封闭图形如阴影所示.
(1)求
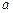 、b、c的值;
、b、c的值;
(2)求阴影面积S关于t的函数S(t)的解析式;
(3)若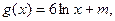 问是否存在实数m,使得
问是否存在实数m,使得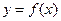 的图象与
的图象与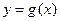 的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.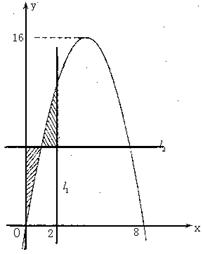

 ;
; .若直线
.若直线 1、
1、 的图象以及
的图象以及
 、b、c的值;
、b、c的值; 问是否存在实数m,使得
问是否存在实数m,使得 的图象与
的图象与 的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
 (Ⅰ)求a、b、c的值 (Ⅱ)求阴影面积S关于t的函数
(Ⅰ)求a、b、c的值 (Ⅱ)求阴影面积S关于t的函数