题目内容
(12分) 已知二次函数
为常数); .若直线
.若直线 1、
1、 2与函数
2与函数 的图象以及
的图象以及 2,y轴与函数
2,y轴与函数 的图象
的图象
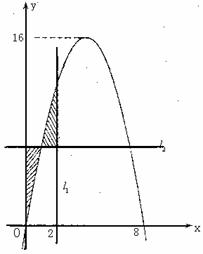
所围成的封闭图形如阴影所示.
(1)求 、b、c的值;
、b、c的值;
(2)求阴影面积S关于t的函数S(t)的解析式;
(3)若 问是否存在实数m,使得
问是否存在实数m,使得 的图象与
的图象与 的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.

【答案】
解:
(I)由图形可知二次函数的图象过点(0,0),(8,0),并且f(x)的最大值为16
则 ,
,
∴函数f(x)的解析式为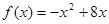
(Ⅱ)由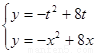 得
得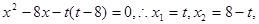
∵0≤t≤2,∴直线l1与f(x)的图象的交点坐标为(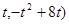
由定积分的几何意义知:
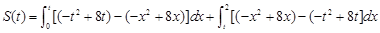
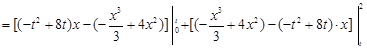
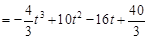 (Ⅲ)令
(Ⅲ)令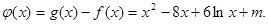
因为x>0,要使函数f(x)与函数g(x)有且仅有2个不同的交点,则函数
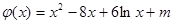 的图象与x轴的正半轴有且只有两个不同的交点
的图象与x轴的正半轴有且只有两个不同的交点
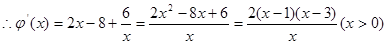
∴x=1或x=3时,
当x∈(0,1)时,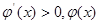 是增函数;
是增函数;
当x∈(1,3)时,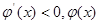 是减函数
是减函数
当x∈(3,+∞)时,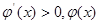 是增函数
是增函数
∴
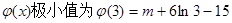
又因为当x→0时,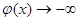 ;当
;当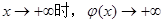
所以要使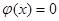 有且仅有两个不同的正根,必须且只须
有且仅有两个不同的正根,必须且只须
即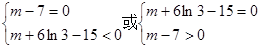 , ∴m=7或
, ∴m=7或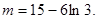
∴当m=7或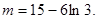 时,函数f(x)与g(x)的图象有且只有两个不同交点。
时,函数f(x)与g(x)的图象有且只有两个不同交点。
【解析】略

练习册系列答案
相关题目

 (Ⅰ)求
(Ⅰ)求 为常数,且
为常数,且 )满足条件:
)满足条件: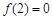 ,且方程
,且方程 有两个相等的实数根.
有两个相等的实数根. 的解析式;
的解析式; 上的最大值和最小值;
上的最大值和最小值;
 使
使 和
和 ,如果存在,求出
,如果存在,求出 的值,如不存在,请说明理由.
的值,如不存在,请说明理由.