摘要：17．设等差数列的前项和为且． (1)求数列的通项公式及前项和公式, (2)设数列的通项公式为.问: 是否存在正整数t.使得 成等差数列?若存在.求出t和m的值,若不存在.请说明理由. [解](1)设等差数列的公差为d. 由已知得 --------2分 即解得--------4分.故. ---6分 知.要使成等差数列.必须.即.--8分.整理得. ----- 11分 因为m.t为正整数.所以t只能取2.3.5.当时.,当时.,当时.. 故存在正整数t.使得成等差数列. ------- 15分
网址：http://m.1010jiajiao.com/timu_id_3206421[举报]
是等比数列
的前
项和，
，
，
成等差数列．
；
，
，
成等差数列；
，
，
成等差数列时，求
的值．(本小题满分15分)
若S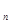
是公差不为0的等差数列
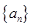的前n项和，且
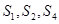成等比数列。
(1)求等比数列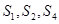的公比；
(2)若
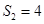，求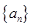的通项公式；
（3）在（2）的条件下，设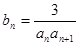
，
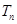是数列
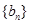的前n项和，求使得
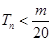对所有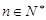
都成立的最小正整数
。
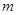查看习题详情和答案>>
中，
，
．
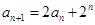．证明：数列
是等差数列；（2）求数列
项和
．
是公差不为0的等差数列
的前n项和，且
成等比数列。
，求
，
是数列
的前n项和，求使得
对所有
都成立的最小正整数
。
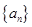中，
，
．
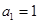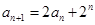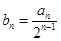．证明：数列
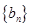是等差数列；（2）求数列
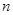项和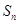
．