摘要:.解法二: 以AB为直径的圆的方程为:
网址:http://m.1010jiajiao.com/timu_id_310188[举报]
 (2013•济宁二模)如图:C、D是以AB为直径的圆上两点,AB=2AD=2
(2013•济宁二模)如图:C、D是以AB为直径的圆上两点,AB=2AD=2| 3 |
(I)求证:平面ACD⊥平面BCD;
(Ⅱ)求三棱锥C-ABD的体积.
(2012•肇庆二模)已知点P是圆F1:(x+
)2+y2=16上任意一点,点F2与点F1关于原点对称.线段PF2的中垂线与PF1交于M点.
(1)求点M的轨迹C的方程;
(2)设轨迹C与x轴的两个左右交点分别为A,B,点K是轨迹C上异于A,B的任意一点,KH⊥x轴,H为垂足,延长HK到点Q使得HK=KQ,连接AQ延长交过B且垂直于x轴的直线l于点D,N为DB的中点.试判断直线QN与以AB为直径的圆O的位置关系.
查看习题详情和答案>>
| 3 |
(1)求点M的轨迹C的方程;
(2)设轨迹C与x轴的两个左右交点分别为A,B,点K是轨迹C上异于A,B的任意一点,KH⊥x轴,H为垂足,延长HK到点Q使得HK=KQ,连接AQ延长交过B且垂直于x轴的直线l于点D,N为DB的中点.试判断直线QN与以AB为直径的圆O的位置关系.
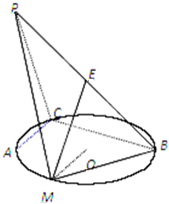 (2012•海淀区二模)如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=
(2012•海淀区二模)如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=| π | 3 |
(Ⅰ)求证:平面MOE∥平面PAC;
(Ⅱ)求证:平面PAC⊥平面PCB;
(Ⅲ)设二面角M-BP-C的大小为θ,求cosθ的值.
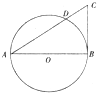 (2013•石家庄二模)选修4-1:几何证明选讲
(2013•石家庄二模)选修4-1:几何证明选讲