摘要：∴SABCD＝
网址：http://m.1010jiajiao.com/timu_id_309752[举报]
如图为一几何体的平面展开图：（1）沿图中虚线将它折叠成原几何体SABCD（使S1、S2、S3、S4重合于S），请画出其直观图；
（2）P、Q 分别是线段SD，AC上的动点，问DP，CQ满足什么条件时PQ∥平面SAB，并证明你的结论．
（3）求该几何体内切球的表面积．
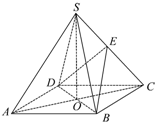如图，在四棱锥SABCD中，底面ABCD是正方形，四个侧面都是等边三角形，AC与BD交于点O，E为侧棱SC上的一点．（1）若E为SC的中点，求证：SA∥平面BDE；
（2）求证：平面BDE⊥平面SAC；
（3）若正方形ABCD边长为2，求四棱锥SABCD的体积．
已知椭圆C：
+
=1(a＞b＞0)的焦点和上顶点分别为F1、F2、B，我们称△F1BF2为椭圆C的特征三角形．如果两个椭圆的特征三角形是相似三角形，则称这两个椭圆为“相似椭圆”，且特征三角形的相似比即为相似椭圆的相似比．已知椭圆C1
+
=1以抛物线y2=4
x的焦点为一个焦点，且椭圆上任意一点到两焦点的距离之和为4．（1）若椭圆C2与椭圆C1相似，且相似比为2，求椭圆C2的方程．
（2）已知点P（m，n）（mn≠0）是椭圆C1上的任一点，若点Q是直线y=nx与抛物线x2=
y异于原点的交点，证明点Q一定落在双曲线4x2-4y2=1上．
（3）已知直线l：y=x+1，与椭圆C1相似且短半轴长为b的椭圆为Cb，是否存在正方形ABCD，使得A，C在直线l上，B，D在曲线Cb上，若存在求出函数f（b）=SABCD的解析式及定义域，若不存在，请说明理由． 查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
（2）已知点P（m，n）（mn≠0）是椭圆C1上的任一点，若点Q是直线y=nx与抛物线x2=
| 1 |
| mn |
（3）已知直线l：y=x+1，与椭圆C1相似且短半轴长为b的椭圆为Cb，是否存在正方形ABCD，使得A，C在直线l上，B，D在曲线Cb上，若存在求出函数f（b）=SABCD的解析式及定义域，若不存在，请说明理由． 查看习题详情和答案>>
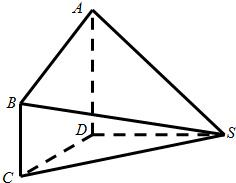如图，在几何体SABCD中，AD⊥平面SCD，BC⊥平面SCD，AD=DC=2，BC=1，又SD=2，，∠SDC=120°．