摘要：于是函数在区间(0.2.(2.2+上是单调增函数,
网址：http://m.1010jiajiao.com/timu_id_30642[举报]
函数y=f（x）的定义域为（-∞，+∞），且具有以下性质：①f（-x）-f（x）=0；②f（x+2）•f（x）=1；③y=f（x）在[0，2]上为单调增函数，则对于下述命题：
（1）y=f（x）的图象关于原点对称
（2）y=f（x）为周期函数且最小正周期是4
（3）y=f（x）在区间[2，4]上是减函数
正确命题的个数为（ ）
（1）y=f（x）的图象关于原点对称
（2）y=f（x）为周期函数且最小正周期是4
（3）y=f（x）在区间[2，4]上是减函数
正确命题的个数为（ ）
| A、0 | B、1 | C、2 | D、3 |
若函数f（x）=
sin2x+2cos2x+m在区间[0，
]上的最大值为2，将函数f（x）图象上所有点的横坐标伸长为原来的2倍（纵坐标不变），再将图象上所有的点向右平移
个单位，得到函数g（x）的图象．
（1）求函数f（x）解析式；
（2）在△ABC中，角A、B、C所对的边分别是a、b、c，又g（
-A）=
，b=2，△ABC的面 积等于3，求边长a的值．
查看习题详情和答案>>
| 3 |
| π |
| 2 |
| π |
| 6 |
（1）求函数f（x）解析式；
（2）在△ABC中，角A、B、C所对的边分别是a、b、c，又g（
| π |
| 2 |
| 8 |
| 5 |
设函数f(x)=sin(ωx+?)(ω＞0，-
＜?＜
)，给出以下四个论断：
①它的图象关于直线x=
对称；
②它的图象关于点（
，0）对称；
③它的最小正周期是π；
④在区间[-
，0]上是增函数．
以其中两个论断作为条件，余下论断作为结论，一个正确的命题：
条件
| π |
| 2 |
| π |
| 2 |
①它的图象关于直线x=
| π |
| 12 |
②它的图象关于点（
| π |
| 3 |
③它的最小正周期是π；
④在区间[-
| π |
| 6 |
以其中两个论断作为条件，余下论断作为结论，一个正确的命题：
条件
3
，结论
．| A、①②⇒③④ |
| B、③④⇒①② |
| C、②④⇒①③ |
| D、①③⇒②④ |
在求导时，可运用对数法：在函数解析式两边求对数得
，两边同时求导得
，于是
。运用此方法可以探求得知
的一个单调递增区间为（ ）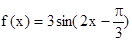
的图象为C：
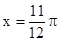对称；
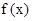在区间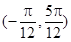
内是增函数；
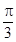个单位长度可以得到图象C；