摘要：可得
网址：http://m.1010jiajiao.com/timu_id_30618[举报]
（Ⅰ）求证：
=
；
（Ⅱ）利用第（Ⅰ）问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1；
（Ⅲ）其实我们常借用构造等式，对同一个量算两次的方法来证明组合等式，譬如：（1+x）1+（1+x）2+（1+x）3+…+（1+x）n=
=
；，由左边可求得x2的系数为C22+C32+C42+…+Cn2，利用右式可得x2的系数为Cn+13，所以C22+C32+C42+…+Cn2=Cn+13．请利用此方法证明：（C2n0）2-（C2n1）2+（C2n2）2-（C2n3）2+…+（C2n2n）2=（-1）nC2nn．
查看习题详情和答案>>
| C | m n |
| n |
| m |
| C | m-1 n-1 |
（Ⅱ）利用第（Ⅰ）问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1；
（Ⅲ）其实我们常借用构造等式，对同一个量算两次的方法来证明组合等式，譬如：（1+x）1+（1+x）2+（1+x）3+…+（1+x）n=
| (1+x)[1-(1+x)n] |
| 1-(1+x) |
| (1+x)n+1-(1+x) |
| x |
（）对变量x, y 有观测数据理力争（
，
）（i=1,2,…，10），得散点图1；对变量u ，v 有观测数据（
，
）（i=1,2,…，10）,得散点图2. 由这两个散点图可以判断 ( )
（A）变量x 与y 正相关，u 与v 正相关 （B）变量x 与y 正相关，u 与v 负相关
（C）变量x 与y 负相关，u 与v 正相关 （D）变量x 与y 负相关，u 与v 负相关
查看习题详情和答案>>
；
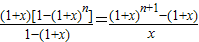；，由左边可求得x2的系数为C22+C32+C42+…+Cn2，利用右式可得x2的系数为Cn+13，所以C22+C32+C42+…+Cn2=Cn+13．请利用此方法证明：（C2n）2-（C2n1）2+（C2n2）2-（C2n3）2+…+（C2n2n）2=（-1）nC2nn．
