Question

（1）利用“五点法”画出函数y=sin(

1

2

x+

π

6

)在长度为一个周期的闭区间的简图．
（2）并说明该函数图象可由y=sinx（x∈R）的图象经过怎样平移和伸缩变换得到的．

Answer 1

分析：（1）先列表如图确定

1

2

x+

π

6

的值，后描点并画图，利用“五点法”画出函数y=sin(

1

2

x+

π

6

)在长度为一个周期的闭区间的简图．
（2）依据y=sinx的图象上所有的点向左平移

π

6

个单位长度，y=sin(x+

π

6

)  再把所得图象的横坐标伸长到原来的2倍（纵坐标不变），得到y=sin(

1

2

x+

π

6

)  或把y=sinx的图象横坐标伸长到原来的2倍（纵坐标不变），得到y=sin

1

2

x的图象．
推出结果．

解答：解：（1）解、先列表，后描点并画图


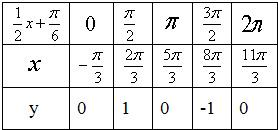
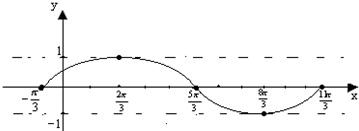
（2）把y=sinx的图象上所有的点向左平移

π

6

个单位长度，得到y=sin(x+

π

6

)的图象，
再把所得图象的横坐标伸长到原来的2倍（纵坐标不变），得到y=sin(

1

2

x+

π

6

)的图象．
或把y=sinx的图象横坐标伸长到原来的2倍（纵坐标不变），得到y=sin

1

2

x的图象．
再把所得图象上所有的点向左平移

π

3

个单位长度，得到y=sin

1

2

(x+

π

3

)，即y=sin(

1

2

x+

π

6

)的图象．

点评：本题考查五点法作函数y=Asin（ωx+φ）的图象，函数y=Asin（ωx+φ）的图象变换，考查计算能力，是基础题．