网址:http://m.1010jiajiao.com/timu_id_302260[举报]
1.D 2.C 3.A 4.B 5.D 6.C 7.C 8.A
9.卷.files/image295.gif) 10.
25 11.
10.
25 11.卷.files/image297.gif) 12.
12.卷.files/image299.gif) 或
或卷.files/image301.gif) 者 13.21 14.3 15.
者 13.21 14.3 15.卷.files/image303.gif)
16.解:(1)卷.files/image305.gif)
卷.files/image307.gif)
卷.files/image309.gif) ……………………………………………(3分)
……………………………………………(3分)
卷.files/image311.gif)
卷.files/image313.gif)
∴卷.files/image168.gif) 值域为
值域为卷.files/image315.gif) …………………………………………………………………(6分)
…………………………………………………………………(6分)
(不同变形参照给分)
(2)因为卷.files/image168.gif) 的周期为
的周期为卷.files/image171.gif)
∴卷.files/image317.gif) ………………………………………………………………(8分)
………………………………………………………………(8分)
∴卷.files/image319.gif)
∴卷.files/image168.gif) 在
在卷.files/image321.gif) 、
、卷.files/image323.gif) 上单调递增,
上单调递增,
在卷.files/image325.gif) 上单调递减。…………………………………………………(12分)
上单调递减。…………………………………………………(12分)
17.解:按一、二、三等奖的顺序,获奖人数有三种情况:
卷.files/image327.gif) ,
,卷.files/image329.gif) ,
,卷.files/image331.gif) …………………………………………………………(1分)
…………………………………………………………(1分)
当获奖人数为卷.files/image327.gif) 时,发奖方式有:
时,发奖方式有:卷.files/image333.gif) (种)…………………(3分)
(种)…………………(3分)
当获奖人数为卷.files/image329.gif) 时,发奖方式有:
时,发奖方式有:卷.files/image335.gif) (种)…………………(5分)
(种)…………………(5分)
当获奖人数为卷.files/image331.gif) 时,发奖方式有:
时,发奖方式有:卷.files/image337.gif) (种)…………………(7分)
(种)…………………(7分)
(1)故恰有2人获一等奖的概率为卷.files/image339.gif) ……………………(9分)
……………………(9分)
(2)故恰有3人获三等奖的概率为卷.files/image341.gif) ……………………(11分)
……………………(11分)
答:(略)………………………………………………………………………(12分)
18.解:(1)证明:依题意知卷.files/image343.gif) ,又∵平面
,又∵平面卷.files/image194.gif) 平面
平面卷.files/image196.gif) ,∴
,∴卷.files/image345.gif) 平面
平面卷.files/image347.gif)
又卷.files/image349.gif) 平面
平面卷.files/image203.gif) ,∴平面
,∴平面卷.files/image194.gif) 平面
平面卷.files/image203.gif) .……………………………(4分)
.……………………………(4分)
(2)解:∵卷.files/image210.gif) ,………………………………………(6分)
,………………………………………(6分)
设P、M到底面卷.files/image196.gif) 的距离分别为
的距离分别为卷.files/image353.gif) 、
、卷.files/image355.gif) ,则
,则
卷.files/image357.gif)
卷.files/image359.gif)
∴卷.files/image361.gif) ,∴
,∴卷.files/image206.gif) 为
为卷.files/image186.gif) 中点。……………………………………………………(8分)
中点。……………………………………………………(8分)
(3)∵卷.files/image365.gif) ,
,卷.files/image367.gif) 平面
平面卷.files/image203.gif) ,
,卷.files/image370.gif) 平面
平面卷.files/image203.gif) ,∴
,∴卷.files/image372.gif) 平面
平面卷.files/image203.gif)
…………………………………………………(10分)
若卷.files/image374.gif) 平面
平面卷.files/image203.gif) ,∵
,∵卷.files/image376.gif) ,∴平面
,∴平面卷.files/image378.gif) 平面
平面卷.files/image203.gif)
这与平面卷.files/image380.gif) 与平面
与平面卷.files/image203.gif) 有公共点
有公共点卷.files/image236.gif) 矛盾
矛盾
∴卷.files/image212.gif) 与平面
与平面卷.files/image203.gif) 不平行……………………………………………………(12分)
不平行……………………………………………………(12分)
(本题也可以用向量法解答)
19.解:(1)由卷.files/image218.gif) ,得
,得卷.files/image385.gif) ,
,
两式相减,得卷.files/image387.gif) ,……………………………………………(3分)
,……………………………………………(3分)
所以数列卷.files/image389.gif) ,
,卷.files/image391.gif) ,
,卷.files/image393.gif) ,…,
,…,卷.files/image395.gif) ,…是以
,…是以卷.files/image397.gif) 为首项,3为公差的等差数列,
为首项,3为公差的等差数列,
即数列卷.files/image224.gif) 为等差数列; ……………………………………………(5分)
为等差数列; ……………………………………………(5分)
又因为卷.files/image216.gif) ,
,卷.files/image401.gif) ,
,
∴卷.files/image403.gif)
∴数列卷.files/image405.gif) ,
,卷.files/image407.gif) ,
,卷.files/image409.gif) ,…,
,…,卷.files/image411.gif) ,…是以
,…是以卷.files/image413.gif) 为首项,3为公差的等差数列,
为首项,3为公差的等差数列,
即数列卷.files/image222.gif) 为等差数列. ……………………………………………………(7分)
为等差数列. ……………………………………………………(7分)
(2)卷.files/image416.gif)
卷.files/image418.gif)
卷.files/image420.gif) ……………………………………………………(10分)
……………………………………………………(10分)
∴卷.files/image422.gif) ,∴
,∴卷.files/image424.gif) ,
,卷.files/image426.gif) ,
,卷.files/image428.gif)
∵数列卷.files/image232.gif) 是等差数列,∴
是等差数列,∴卷.files/image431.gif) ,
,
∴卷.files/image433.gif) ,
,
解得:卷.files/image435.gif) ,
,卷.files/image437.gif) (舍去).……………………………………………(13分)
(舍去).……………………………………………(13分)
20.解(1)令卷.files/image439.gif) ,
,卷.files/image441.gif) .
.
由题意得:卷.files/image443.gif)
又卷.files/image445.gif) ,所以
,所以卷.files/image447.gif) ,
,
所以卷.files/image449.gif) …………………………………(4分)
…………………………………(4分)
(2)∵卷.files/image451.gif) ,∴
,∴卷.files/image453.gif) ,于是
,于是卷.files/image455.gif) ,
,
∴卷.files/image457.gif) ,
,
∴椭圆E的方程为卷.files/image459.gif) …………………………………………………(5分)
…………………………………………………(5分)
从而卷.files/image461.gif) ,
,卷.files/image463.gif)
设点M、N、G的坐标依次为卷.files/image465.gif) 、
、卷.files/image467.gif) 、
、卷.files/image469.gif) ,
,
∵卷.files/image258.gif) ,∴
,∴卷.files/image471.gif) ,
,
∴卷.files/image473.gif) ………………………………………………………………(7分).
………………………………………………………………(7分).
又卷.files/image475.gif) ,
,
卷.files/image477.gif)
且卷.files/image266.gif) ,
,
∴卷.files/image480.gif)
即得卷.files/image482.gif) . ………………………………………………(9分)
. ………………………………………………(9分)
又卷.files/image484.gif) ,
,
故得卷.files/image486.gif) .……………………………………………(*)(10分)
.……………………………………………(*)(10分)
因卷.files/image253.gif) 不垂直于
不垂直于卷.files/image251.gif) 轴,设直线
轴,设直线卷.files/image253.gif) 的方程为
的方程为卷.files/image490.gif) ,与椭圆
,与椭圆卷.files/image238.gif) :
:卷.files/image459.gif) 联立得:
联立得:
卷.files/image493.gif)
∵点卷.files/image249.gif) 在椭圆内部,
在椭圆内部,
∴直线卷.files/image253.gif) 必与椭圆有两个不同交点.
必与椭圆有两个不同交点.
方程卷.files/image493.gif) 有两个不等实数根
有两个不等实数根卷.files/image281.gif) ,
,卷.files/image283.gif)
则由根与系数的关系,得
卷.files/image497.gif) ,
,卷.files/image499.gif) ,
,
代入(*)得卷.files/image501.gif)
整理,得卷.files/image503.gif) ,即
,即卷.files/image505.gif)
∴存在这样的定点卷.files/image505.gif) 满足题设.…………………………………………(13分)
满足题设.…………………………………………(13分)
21.解:(1)∵卷.files/image268.gif) ,
,
∴卷.files/image507.gif) ,即
,即卷.files/image509.gif) 。又
。又卷.files/image511.gif) ,
,
∴卷.files/image279.gif) 即为
即为卷.files/image513.gif) ,
,
∴卷.files/image515.gif)
∵卷.files/image272.gif) ,∴
,∴卷.files/image518.gif) .
.
解得卷.files/image520.gif) ,
,
又∵方程卷.files/image522.gif) ,(
,(卷.files/image272.gif) )有两根,∴
)有两根,∴卷.files/image525.gif)
而卷.files/image527.gif) 恒成立,
恒成立,
∴卷.files/image529.gif) 的取值范围是
的取值范围是卷.files/image531.gif) .………………………………………………(6分)
.………………………………………………(6分)
(2)∵卷.files/image281.gif) 、
、卷.files/image283.gif) 是方程
是方程卷.files/image285.gif) 的两根即
的两根即卷.files/image533.gif) 的两根为
的两根为卷.files/image281.gif) 、
、卷.files/image283.gif)
∴卷.files/image535.gif) ,
,卷.files/image537.gif)
∴卷.files/image539.gif)
卷.files/image541.gif)
卷.files/image543.gif)
∵卷.files/image520.gif) ,∴当且仅当
,∴当且仅当卷.files/image545.gif) ,即
,即卷.files/image547.gif) 时,
时,卷.files/image549.gif) 取最小值.
取最小值.
即卷.files/image547.gif) 时,
时,卷.files/image291.gif) 最小. ………………………………………………(10分)
最小. ………………………………………………(10分)
此时卷.files/image552.gif) ,
,卷.files/image554.gif) ,
,
令卷.files/image285.gif) ,得
,得卷.files/image557.gif) ,
,卷.files/image559.gif) ,
,
∵卷.files/image289.gif) ,∴
,∴卷.files/image251.gif) 、
、卷.files/image168.gif) 、
、卷.files/image276.gif) 的变化情况如下表
的变化情况如下表
卷.files/image251.gif)
卷.files/image565.gif)
卷.files/image567.gif)
卷.files/image569.gif)
卷.files/image571.gif)
卷.files/image573.gif)
卷.files/image168.gif)
卷.files/image575.gif)
卷.files/image571.gif)
卷.files/image577.gif)
卷.files/image571.gif)
卷.files/image575.gif)
卷.files/image276.gif)
ㄊ
极大 值
ㄋ
极小值
ㄊ
∴由表知:卷.files/image276.gif) 的极大值为
的极大值为卷.files/image579.gif) ,极小值为
,极小值为卷.files/image581.gif) ,由题知
,由题知卷.files/image583.gif) 。
。
解得卷.files/image585.gif) ,此时
,此时
①过一点有且仅有一个平面与已知直线垂直;
②若平面外两点到平面的距离相等,则过这两点的直线必平行于该平面;
③两条相交直线在同一平面内的射影必为相交直线;
④两个互相垂直的平面,一个平面内的任一直线必垂直于另一平面的无数条直线.
其中正确的命题是( )
①a∥α,b?β;
②a⊥α,b∥β;
③a⊥α,b⊥β;
④a∥α,b∥β且a与α的距离等于b与β的距离.
①如果一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②如果一条直线和两个平行平面中的一个平面垂直,那么这条直线也和另一个平面垂直;
③如果一条直线和两个互相垂直的平面中的一个平面垂直,那么这条直线一定平行于另一个平面;
④如果两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中为真命题的是( )

 ,
,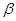 为两个互相垂直的平面,a、b为一对异面直线,下列条件:
为两个互相垂直的平面,a、b为一对异面直线,下列条件: ;②a⊥
;②a⊥ ;③a⊥
;③a⊥ ;④a//
;④a//