题目内容
5、α，β为两个互相垂直的平面，a、b为一对异面直线，下列条件：
①a∥α、b?β；②a⊥α．b∥β；
③a⊥α．b⊥β；④a∥α、b∥β且a与α的距离等于b与β的距离，其中是a⊥b的充分条件的有（ ）
①a∥α、b?β；②a⊥α．b∥β；
③a⊥α．b⊥β；④a∥α、b∥β且a与α的距离等于b与β的距离，其中是a⊥b的充分条件的有（ ）
分析：判断线与线、线与面、面与面之间的关系，可将线线、线面、面面平行（垂直）的性质互相转换，进行证明，也可将题目的中直线放在空间正方体内进行分析．
解答：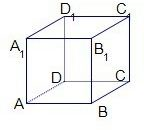
解：如图令平面AC为α，平面BC1为β．
①若a=A1B1，b=B1C，则a，b不垂直，
②若a=BB1，b=AD1，则a，b不垂直，
③a⊥α则a∥β或a?β，又∵b⊥β∴a⊥b，
④若a=A1B1，b=A1D，则a，b不垂直．
故只有③是a⊥b的充分条件，
故答案为C．
解：如图令平面AC为α，平面BC1为β．①若a=A1B1，b=B1C，则a，b不垂直，
②若a=BB1，b=AD1，则a，b不垂直，
③a⊥α则a∥β或a?β，又∵b⊥β∴a⊥b，
④若a=A1B1，b=A1D，则a，b不垂直．
故只有③是a⊥b的充分条件，
故答案为C．
点评：在判断空间线面的关系，常常把他们放在空间几何体中来直观的分析，在判断线与面的平行与垂直关系时，正方体是最常用的空间模型，大家一定要熟练掌握这种方法．
练习册系列答案
相关题目
为两个互相垂直的单位向量，求
，
为两个互相垂直的平面，
、b为一对异面直线，下列条件：
；②
；③
；④
，
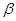为两个互相垂直的平面，a、b为一对异面直线，下列条件：
；②a⊥
；③a⊥
；④a//