网址:http://m.1010jiajiao.com/timu_id_300685[举报]
一.1.D 2.B 3.B 4.B 5.B 6.C 7.C 8.A 9.C 10.C
二.11. 5或%20.files/image079.gif) 12. 2倍 13. 70º 14.
25cm2 15. n.
2n. 4n. n 16.
12. 2倍 13. 70º 14.
25cm2 15. n.
2n. 4n. n 16.%20.files/image081.gif)
三.
17.解:原式=(%20.files/image083.gif) -
-%20.files/image085.gif) ×
×%20.files/image087.gif) …2分
…2分
%20.files/image094.gif) =-
=-%20.files/image096.gif) =-
=-%20.files/image098.gif) …5分
…5分
18.解:
(1)按要求作出梯形%20.files/image100.gif) (2分)
(2分)
(2) 按要求作出梯形%20.files/image047.gif) (4分)
(4分)
按要求作出梯形%20.files/image049.gif) (6分)
(6分)
19. (1)证明:在平行四边形ABCD中,
∵ AB∥CD, ∴∠BAF=∠CEF,∠ABF=∠ECF,
∵ AB=CD,CE=CD, ∴ AB=CE,
∴ △AFB≌△EFC
(2)解:∵ ED=2CD=2AB,∴ %20.files/image104.gif) ,
,
∵ AB∥CD, ∴ %20.files/image106.gif) ,又BD=12
,又BD=12
所以,DG=%20.files/image108.gif) BD=8 cm。
BD=8 cm。
20 (1)0.24 , 50 ;(2)(高度为F组的2倍);(3)432;
21. 解: (1)由图可知洗衣机的进水时间是4分钟,.清洗时洗衣机中的水量是40升 (3分)
(2)①∵排水的时间是2分钟, 排水速度为每分钟19升,
∴排水结束时洗衣机中剩下的水量是%20.files/image110.gif) (升) (4分)
(升) (4分)
%20.files/image112.gif) ②
②
∵%20.files/image114.gif) ,
,%20.files/image116.gif)
设%20.files/image118.gif) 的函数表达式为
的函数表达式为%20.files/image120.gif)
%20.files/image124.gif) (9分)
(9分)
∴%20.files/image126.gif) (
(%20.files/image128.gif) ) (8分)
) (8分)
22.(1)设小路的宽为xm,则(16-2x)(12-2x)=%20.files/image130.gif) ×16×12,解得x=2,或x=12(舍去). ∴x=2,故小明的结果不对.
×16×12,解得x=2,或x=12(舍去). ∴x=2,故小明的结果不对.
(2)四个角上的四个扇形可合并成一个圆,设这个圆的半径为rm,
%20.files/image131.gif) 故有
故有%20.files/image133.gif) r2=
r2=%20.files/image130.gif) ×16×12,解得r≈5.5m.
×16×12,解得r≈5.5m.
(3)依此连结各边的中点得如图的设计方案.
23、(1)(1)证明:∵AB为⊙O的直径,CD⊥AB,
∴∠AEB=∠ADH=90°,
∴∠C+∠CHE=90°,∠A+∠AHD=90°,
∵∠AHD=∠CHE,∴∠A=∠C,
∵∠ADH=∠CDB=90°,
∴△AHD∽△CBD
(2)设OD=x,则BD=1-x,AD=1+x
证Rt△AHD∽Rt△CBD
则HD : BD=AD : CD
即HD : (1-x)=(1+x) : 2
即HD=%20.files/image135.gif)
在Rt△HOD中,由勾股定理得:
所以HD+HO=%20.files/image135.gif) +
+%20.files/image139.gif) =1
=1
24. (1)在RtΔABC中, ,
又因为点B在x轴的负半轴上,所以B(-2,0)
(2)设过A,B,D三点的抛物线的解析式为 ,
将A(0,6),B(-2,0),D(4,6)三点的坐标代入得
%20.files/image142.gif)
%20.files/image144.gif) 解得
解得 %20.files/image146.gif) 所以
所以 %20.files/image148.gif)
(3)在抛物线上存在点P1(0,6)或P2(4,6),使SΔPBC=%20.files/image150.gif) S梯形ABCD
S梯形ABCD
25、 解:(1)在Rt△CDF中,sinC=%20.files/image075.gif) ,CD=x,
,CD=x,
∴DF=CD• sinC=%20.files/image075.gif) x,CF=
x,CF=%20.files/image154.gif)
∴BF=18-%20.files/image156.gif) 。
。
(2)∵ED∥BC,∴%20.files/image158.gif) ,
,
∴ED=%20.files/image160.gif)
∴S=%20.files/image150.gif) ×DF×(ED+BF)
×DF×(ED+BF)
=%20.files/image163.gif)
(3)由S1=2S2,得S1=%20.files/image108.gif) S
S
解这个方程,得:x1=10,x2=0(不合题意,舍去)
所以,当x=10时,S1=2S2。
在一块长16m、宽12m的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半。下面分别是小明和晓颖的设计方案。
小明说:我的设计方案如图(1),其中花园四周小路的宽度相等。通过解方程,我得到小路的宽为2m或12m。
晓颖说:我的设计方案如图(2),其中花园每个角上的扇形相同。
(1)你认为小明的结果对吗?请说明理由。
(2)请你帮助晓颖求出图(2)中的![]() 。(
。(![]() 取3,结果保留根号)
取3,结果保留根号)
(3)你还有其他的设计方案吗?请在图(3)的矩形中画出你的设计草图,并加以说明。

在一块长![]() 、宽
、宽![]() 的矩形荒地上,要建造一个学生实验植物园,要求植物园所占面积为荒地面积的一半. 下面分别是小明和小颖的设计方案.
的矩形荒地上,要建造一个学生实验植物园,要求植物园所占面积为荒地面积的一半. 下面分别是小明和小颖的设计方案.
小明说:我的设计方案如图(1),其中园地四周小路的宽度相等. 通过解方程,我得到小路的宽为![]() 或
或![]() .
.
小颖说:我的设计方案如图(2),其中植物园为阴影部分,荒地的每个角上的扇形相同.
(1)你认为小明的结果对吗?请说明理由;
(2)请你帮助小颖求出图中的![]() (精确到0.1m);
(精确到0.1m);
(3)你还有其他的设计方案吗?请在下边的矩形中画出你的设计草图,并加以说明.


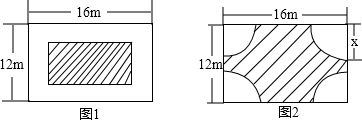
小明说:我的设计方案如图1,其中花园四周小路的宽度相等.通过解方程,我得到小路的宽为2m或12m.
小颖说:我的设计方案如图2,其中花园中每个角上的扇形相同.
(1)你认为小明的结果对吗?请说明理由.
(2)请你帮助小颖求出图中的x(精确到0.1m).
(3)你还有其他的设计方案吗?请在下边的矩形中画出你的设计草图,并加以说明.
 查看习题详情和答案>>
查看习题详情和答案>>
%20.files/image089.gif) ×
×%20.files/image092.gif) …4分
…4分 %20.files/image122.gif)
%20.files/image137.gif)
%20.files/image168.gif) =
=%20.files/image170.gif)